Question

How to factorize (y-2)^2 - 24(y-2) + 144 by taking out (y-2) first?

Answer 1

`(y-14)^2`

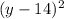
Explanation:

Given quadratic expression:

`(y-2)^2 - 24(y-2) + 144`

Factor out the common term (y - 2) from the first and second terms of the given expression:

`(y-2)\left[(y-2)-24\right]+144`

Simplify the second set of brackets:

`(y-2)\left[y-2-24\right]+144`

`(y-2)\left[y-26\right]+144`

`(y-2)(y-26)+144`

Expand the brackets:

`y^2-26y-2y+52+144`

`y^2-28y+196`

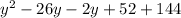
Find two numbers that sum to -28 and multiply to 196.

These two numbers are -14 and -14.

Rewrite the middle term as the sum of these two numbers:

`y^2-14y-14y+196`

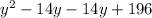
Factor the first two terms and the last two terms separately:

`y(y-14)-14(y-14)`

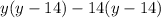
Factor out the common term (y - 14):

`(y-14)(y-14)`

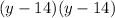
An expression multiplied by itself can be written as the square of the expression. Therefore:

`\large\boxed{(y-14)^2}`