Question

T(t) models the daily high temperature (in °C) in Santiago, Chile, t days after the hottest day of the year.

Here, t is entered in radians.
T(t) = 7.5 cos(2π t/365) + 21.5
What is the second time after the hottest day of the year that the daily high temperature is 20°C?
Round your final answer to the nearest whole day.
____ days

Answer 1

To find a second time when the temperature is 20°C after the hottest day of the year, we need to solve the equation T(t) = 20. Rearranging the equation and using inverse cosine, we can find the value of t in radians and then convert it to days.

Step-by-step explanation:

To find the second time after the hottest day of the year that the daily high temperature is 20°C, we need to find the values of t that satisfy the equation T(t) = 20. Here, T(t) is given by T(t) = 7.5 cos(2π t/365) + 21.5. Rearranging the equation, we have 7.5 cos(2π t/365) = -1.5. Dividing both sides by 7.5, we get cos(2π t/365) = -1/5. Taking the inverse cosine of both sides, we find t = 365 cos^(-1)(-1/5) / (2π). Evaluating this expression, we can find the value of t in radians, which we then convert to days by multiplying by 365/(2π).

Answer 2

The second time after the hottest day of the year is 103 days.

Finding the temperature difference using trigonometry functions.

To find the second time temperature after the hottest day of the year, we need to follow these steps.

Given that the equation between the temperature T and time t is:

`T(t)=7.5 \ cos \ ((2 \pi )/(365)t) + 21.5`

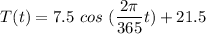
To find time t when temperature (T) = 20°C, we need to replace 20°C for T in the above equation.

`20 =7.5 \ cos \ ((2 \pi )/(365)t) + 21.5`

`20 -21.5=7.5 \ cos \ ((2 \pi )/(365)t)`

`-1.5=7.5 \ cos \ ((2 \pi )/(365)t)`

`(-1.5)/(7.5)=\ cos \ ((2 \pi )/(365)t)`

`\ cos \ ((2 \pi )/(365)t) = -0.2`

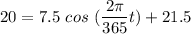
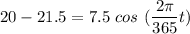
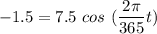
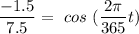
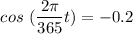
Taking the inverse of cosine on each side of the above equation, we have:

`(2 \pi )/(365)t =cos^(-1)( -0.2)`

`(2 \pi \ t)/(365) =cos^(-1)( -0.2)`

`(2 \pi \ t )/(365) = 1.7722`

`t = 1.7722* (365)/(2 \pi)`

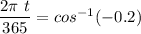
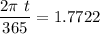
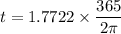
t = 102.95 days

t ≅ 103 days.