Question

If V(r)=4/3 pi r^3, find V(2r)/V(r)

Answer 1

`(V(2r))/(V(r)) =8`

Explanation:

To find V(2r)/V(r), we can substitute the values into the given formula for volume and calculate the ratio:

`(V(2r))/(V(r)) = ((4)/(3) \pi (2r)^3)/((4)/(3) \pi (r)^3)`

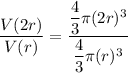
Simplify the expression:

`(V(2r))/(V(r)) = ((2r)^3)/((r)^3)`

`(V(2r))/(V(r)) = (8r^3)/(r^3)`

`(V(2r))/(V(r)) =8`

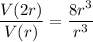
Therefore, V(2r)/V(r) = 8.

This means that the volume of a sphere with radius 2r is 8 times larger than the volume of a sphere with radius r.