Question

Determine the behavior of the graph on either side of any vertical asymptotes, if one exists. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice O A. It approaches [infinity] on one side of the asymptote(s) at x = and - [infinity] on the other. It approaches either [infinity] or -[infinity] on both sides of the asymptote(s) at x = (Type integers or simplified fractions. Use a comma to separate answers as needed. Type each answer only once.) O B. It approaches either [infinity] or -[infinity] on both sides of the asymptote(s) at x = (Type an integer or a simplified fraction. Use a comma to separate answers as needed. Type each answer only once.) O C. It approaches [infinity] on one side of the asymptote(s) at x = and - [infinity] on the other. (Type an integer or a simplified fraction. Use a comma to separate answers as needed. Type each answer only once.) O D. The function has no vertical asymptote.

Answer 1

The correct choice is O C. It approaches [infinity] on one side of the asymptote(s) at x = and - [infinity] on the other.

Explanation:

Vertical asymptotes occur when the function approaches infinity or negative infinity as x approaches a certain value. In this case, option C is the correct choice, indicating that the graph approaches infinity on one side of the vertical asymptote and negative infinity on the other.

Consider a vertical asymptote at x = a. As x approaches a from the left
`(x → a^-)`, if the function approaches positive infinity, it means the graph goes upward without bound. If x approaches a from the right
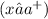`(x → a^+)`, and the function approaches negative infinity, it means the graph goes downward without bound.

Mathematically, for a vertical asymptote at x = a:

`\[ \lim_{{x \to a^-}} f(x) = \infty \]`

`\[ \lim_{{x \to a^+}} f(x) = -\infty \]`

This behavior is typical for functions with vertical asymptotes. Understanding this helps in visualizing how the graph behaves around the vertical asymptotic point. So, the correct choice is option C, as it precisely describes the behavior of the graph on either side of the vertical asymptote.