Final answer:
The domain for each function presented varies based on the type of function and any restrictions given. Linear and polynomial functions generally have domains of all real numbers, while rational functions and functions involving square roots may have restrictions that exclude certain values to prevent division by zero or taking the square root of a negative number.
Step-by-step explanation:
The domain in mathematics generally refers to the set of all possible input values (typically x-values) for which a function is defined. Looking at the various functions in this question, we can establish domains based on the type of function and any restrictions stated in the function's equation.
Here are some general rules that will help in determining the domain:
- For linear functions such as f(x) = -11x + 7, the domain is all real numbers, which is written in interval notation as (-∞, ∞).
- For polynomial functions like f(x) = x¹⁰ + 1, the domain is similarly all real numbers.
- Rational functions like f(x) =
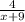 have domains that exclude values making the denominator zero; hence the domain here is (-∞, -9) ∪ (-9, ∞).
have domains that exclude values making the denominator zero; hence the domain here is (-∞, -9) ∪ (-9, ∞). - For a function with a square root, such as f(x) = √{x + 7}, the domain includes all x-values that ensure the expression under the square root is non-negative, which in this case is [-7, ∞).
- If no restrictions are placed on x, such as with a constant function like f(x) = -4, the domain is all real numbers.