Question

10. a) An angle is 21° more than twice its complement. Find it.​

Answer 1

23° and 67°

Explanation:

Key Info

The sum of the measures of two complementary angles is always 90°.

So, when setting up our equation, the right-hand side is going to be 90.

Now, let's call the unknown angle x. Then,

`\rm{2x+x+21=90}`

Combine like terms:

`\rm{3x+21=90}`

Subtract 21 from both sides:

`\rm{3x=69}`

Lastly, divide both sides by 3:

`\boxed{\rm{x=23}}`

This is one of the angles. Now, since they are complementary, we can easily find the other angle by subtracting 23 from 90:

`\rm{other\:angle=90-23}`

`\rm{other\;angle=67^o}`

Therefore, the two angles are 23 and 67.

Answer 2

The angle measures 67°, and its complement measures 23°.

Explanation:

Problem Statement:

The measure of an angle is 21° more than twice the measure of its complement. Find the measure of each angle.

Let's call the measure of the angle "θ" degrees and the measure of its complement "θ_c" degrees.

`\hrulefill`

According to the problem statement, the angle is 21° more than twice its complement. We can write this relationship as an equation:

`\Longrightarrow \theta=2\theta_c+21\textdegree`

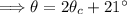
Since the sum of an angle and its complement is 90 degrees, we can write another equation:

`\Longrightarrow \theta + \theta_c = 90\textdegree`

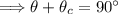
Now we have a system of equations with two unknowns (θ and θ_c):

`\Longrightarrow \left\{\begin{array}{ccc}\theta =2\theta_c+21\textdegree\\\theta+\theta_c=90\textdegree\\\end{array}\right`

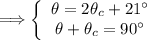
Substitute the value of 'θ' from the first equation into the second equation:

`\Longrightarrow 2\theta_c+21\textdegree+\theta_c=90\textdegree`

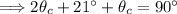
Combine like terms:

`\Longrightarrow 3\theta_c+21\textdegree=90\textdegree`

Subtract 21 from both sides:

`\Longrightarrow 3\theta_c+21\textdegree-21\textdegree=90\textdegree-21\textdegree\\\\\\\\\Longrightarrow 3\theta_c=69\textdegree`

Divide both sides by 3:

`\Longrightarrow \frac33\theta_c=(69\textdegree)/(3)\\\\\\\\\therefore \boxed{\boxed{\theta_c=23\textdegree}}`

Now that we know the value of the complement θ_c is 23 degrees, we can find the value of the angle θ using the first equation:

`\Longrightarrow \theta=2(23\textdegree)+21\textdegree\\\\\\\\\Longrightarrow \theta=46\textdegree+21\textdegree\\\\\\\\\therefore \boxed{\boxed{\theta = 67 \textdegree}}`

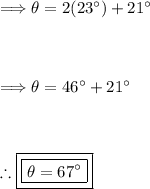
Thus, the angle measures 67 degrees, and its complement measures 23 degrees.

`\hrulefill`

Additional Information:

System of Equations: In this problem, we're dealing with a system of equations, which consists of a group of equations involving multiple variables. The objective is to discover the specific values of these variables that make all the equations true at the same time.

Complementary Angles: Complementary angles are a pair of angles that, when added, yield a total of 90 degrees. In other words, if you have two angles and their measurements, and the sum of those measurements equals 90 degrees, these angles are termed complementary to one another.