Question

Find the surface area of the following figures 16 ft 13 ft 12ft 19ft

Please help me solve number 3! And if i got #2 incorrect, please help me fix that one too.

Answer 1

1192 ft²

Explanation:

Figure 3 is a trapezoidal prism.

The total surface area of a trapezoidal prism is made up of 2 congruent trapezoid bases and 4 rectangular faces connecting the bases.

The formula for the area of a trapezoid is:

`\boxed{S.A.=(1)/(2)(a+b)h}`

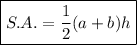
where a and b are the bases, and h is the height.

From observation of the given diagram, the bases are 16 ft and 19 ft, and the height is 12 ft. Therefore, the area of each trapezoid base is:

`\begin{aligned}\textsf{Area of trapezoid base}&=(1)/(2)(16+19)\cdot 12\\\\&=(1)/(2)(35)\cdot 12\\\\&=17.5\cdot 12\\\\&=210\; \sf ft^2\end{aligned}`

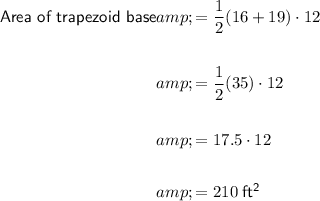
To calculate the areas of all the rectangular faces, we first need to calculate the slant (s) of the trapezoid base by using the Pythagoras Theorem:

`\begin{aligned}s^2&=(19-16)^2+12^2\\s^2&=3^2+12^2\\s^2&=9+144\\s^2&=153\\s&=√(153)\end{aligned}`

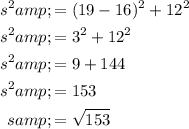
The area of a rectangle is the product of its width and length.

Therefore, the sum of the areas of the rectangular faces is:

`\begin{aligned}\textsf{Area of rectangular faces}&=16\cdot13+12\cdot13+19\cdot13+√(153)\cdot13\\&=208+156+247+13√(153)\\&=771.801119...\\&=772\; \sf ft^2\;(nearest\;foot)\end{aligned}`

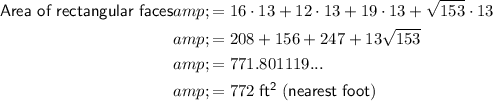
To find the total surface area of the given trapezoidal prism, sum the area of the two trapezoid bases and the area of the rectangular faces:

`\begin{aligned}\textsf{Total S.A.}&=2 \cdot 210+772\\&=420+772\\&=1192\; \sf ft^2\end{aligned}`

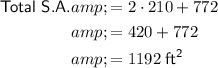
Therefore, the total surface area of the given trapezoidal prism is 1192 ft², rounded to the nearest foot.