Question

Use the Shell Method to compute the volume of the solids obtained by rotating the region enclosed by the graphs of the functions y = x^2, y = 8 – x^2 and to the right of x = 0 about the y-axis. V = 1

Answer 1

Explanation:

When using the shell method to find volume of a solid, your "representative rectangle" will be parallel to the axis of rotation. The formula for the shell method is as follows:

`V=2\pi\int\limits^a_b {p(x)*h(x)} \, dx`

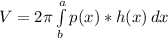
where a and b are the bounds of integration in terms of where the functions intersect each other at the same x value, p(x) is the distance in terms of x from the axis of rotation to the point of intersection, and h(x) is the height of the representative rectangle. For us, the functions intersect at the x-value of 2, so the interval in terms of x is [0, 2], p(x) = x, and h(x), the height of the rectangle is the upper function minus the lower. Here is our particular formula using the given information:

`V=2\pi\int\limits^2_0 {[x(8-x^2-x^2)} \, dx`

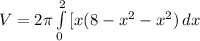
which simplifies to

`V=2\pi\int\limits^2_0 {8x-2x^2} \, dx`

The antiderivative of this gives us

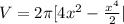`V=2\pi[4x^2-(x^4)/(2)|` from F(2)-F(0) which is, in terms of pi,

16π