Question

Use the definite integral to find the area between the x-axis and the graph of f(x) over the indicated interval,

​F(x) = 2x + 7 [1, 5]

Answer 1

Explanation:

`\int\limits^5_1 {2x+7} \, dx`

The First Fundamental Theorem of Calculus tells us that F(b)-F(a) is the antiderivative of the derivative, which is the function itself. The antiderivative of 2x + 7 follows the pattern

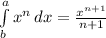`\int\limits^a_b {x^n} \, dx =(x^(n+1))/(n+1)` evaluated for F(5) - F(1).

Our antiderivative for 2x is

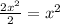`(2x^2)/(2)=x^2` and the antiderivative for 7 is 7x.

`F=x^2+7x` over the interval from 1 to 5.

F(5) - F(1) = [25 + 35] - [1 + 7] = 60 - 8 = 52