Question

How do you prove that 19n + 16 cannot be a perfect square for any three consecutive integers n?

Answer 1

To prove 19n + 16 cannot be a perfect square for any three consecutive integers (n), we can apply a proof by contradiction. We can assume first that a perfect square exists in the form of 19n + 16, then explain how this is contradictory.

Assumption: For an integer, n, there exists a perfect square in the form of 19n + 16.

Let
`x^(2)` represent a perfect square, where x is an integer. This makes our equation:

19n + 16 =
`x^(2)`

To isolate n, we can rearrange the equation:

n =
`(x^(2) - 16)/(19)`

Because
`x^(2)` and 16 are both perfect squares,
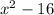`x^(2) - 16` must also represent a perfect square. The problem with this, however, is that dividing a perfect square by 19 is unlikely to result in an integer, unless it is divisible by 19. We can prove this to be a contradiction on account of three consecutive integers (1, 2, and 3):

When
`x = 1`:

`n =(1^(2) - 16 )/(19) = (-15)/(19)`

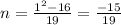
When
`x = 2`:

`n = (2^(2)-16 )/(19) = (-12)/(19)`

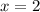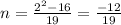
When
`x = 3`:

`n = (3^(2) - 16)/(19) = (-7)/(19)`

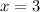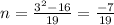
Because none of the final fractions are values of x, we have shown by three examples of consecutive integers that 19n + 16 cannot be a perfect square for any three consecutive integers. Therefore, this is a contradiction.

Answer 2

Answer and Explanation:

We can prove that the value of the expression
`19n+16` cannot be a perfect square for any three consecutive integers
`n` using contradiction.

We can represent the three consecutive integers as:
`n`,
`n+1`, and
`n+2`.

If
`19n + 16` is a perfect square, which we can call
`a^2`, then
`19(n+1) + 16` and
`19(n+2) + 16` must also be perfect squares. If we express these in terms of
`a^2`, we get:

• 
  `19n + 16 = a^2`
• 
  `19(n+1) + 16 = 19n + 19 + 16 = (19n + 16) + 19 = a^2 + 19`
• 
  `19(n+2) + 16 = 19n + 2 \cdot 19 + 16 = (19n + 16) + 2\cdot 19 = a^2 + 2 \cdot 19`

We can see that the difference between each consecutive equation (listed above) is 19. For
`19n+16` to be a perfect square for any three consecutive integers
`n`,
`a^2 + 19` and
`a^2 + 2 \cdot 19` must also be perfect squares.

However, this is not possible because the difference between any two consecutive perfect squares always increases. Therefore,
`19n + 16` cannot be a perfect square for any three consecutive integers
`n`.