Question

50 POINTS! Vectors u, v, and w are shown in the graph. What are the magnitude and direction of u + v + w? Round the magnitude to the thousandths place and the direction to the nearest degree.

Answer 1

The answer is c :48.786; 152°

Answer 2

C) 48.786, 152°

Explanation:

To add the vectors u, v and w, we first need to rewrite each vector in component form (where vectors are represented using the unit vectors i and j along the x and y axes).

The (x, y) components of a vector, given its magnitude (r) and direction (θ), are (r cos θ, r sin θ), where θ is measured in the anticlockwise direction from the positive x-axis.

Every vector in two dimensions is made up of horizontal and vertical components, so any vector can be expressed as a sum of i and j unit vectors. Therefore, the i + y form of a vector is:

• (r cos θ) i + (r sin θ) j

So, the component form of the given vectors are:

`\mathbf{u}=80 \cos 230^(\circ)\textbf{i}+80 \sin 230^\circ}\textbf{j}`

`\mathbf{v}=60 \cos 120^(\circ)\textbf{i}+60 \sin 120^\circ}\textbf{j}`

`\mathbf{w}=50 \cos 40^(\circ)\textbf{i}+50 \sin 40^\circ}\textbf{j}`

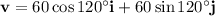
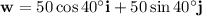
Sum the vectors:

`\mathbf{R}=\mathbf{u}+\mathbf{v}+\mathbf{w}\\\\\mathbf{R}=(80 \cos 230^(\circ)+60 \cos 120^(\circ)+50 \cos 40^(\circ))\textbf{i}+(80 \sin 230^\circ}+60 \sin 120^\circ}+50 \sin 40^\circ})\:\textbf{j}\\\\\mathbf{R}=-43.1207866\:\textbf{i}+22.8173493\:\textbf{j}`

`\textsf{For a vector\;\;$\mathbf{a} = x\mathbf{i} + y\mathbf{j}$, its magnitude is\;\;$||\mathbf{a}|| = √(x^2+y^2)$.}`

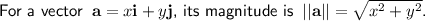
Calculate the magnitude of the resultant vector ||R||:

`\mathbf=√((-43.1207866)^2+(22.8173493)^2)\\\\\mathbfR=48.7855887...\\\\\mathbf=48.786`

The direction θ can be found by finding the angle with the horizontal, which is given by:

`\boxed{\theta=\tan^(-1)\left((y)/(x)\right)}`

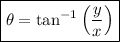
As the resultant vector is in quadrant II (since the i component is negative and the j component is positive), we need to add 180° to the value of tan⁻¹(y/x). Therefore:

`\theta=\tan^(-1)\left((22.8173493)/(-43.1207866)\right)+180^(\circ)`

`\theta=-27.8855396+180^(\circ)`

`\theta=152.114460^(\circ)`

`\theta=152^(\circ)\; \sf (nearest\;degree)`

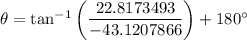
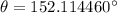
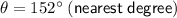
Therefore:

• Magnitude = 48.786
• Direction = 152°