Question

This page is hard!! PLSS HELP ILL GIVE ALL THE POINTS I CAN FOR ALL PLEASE

Answer 1

For 1st Question:

• Equation:
  `\sf n + (n)/(2)= 90`
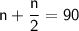
• Nate picked 60 apples.
• Laura picked 30 apples.

For 2nd Question:

• Equation:
  `\sf \sf (b - 12) + b = 98`
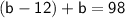
• Jacket A costs $43
• Jacket B costs $55.

For 3rd Question:

• Equation:
  `\sf \sf (b - 12) + b = 98`
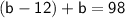
• Jacket A costs $43
• Jacket B costs $55.

Explanation:

For 1st Question:

Let's use the following variables:

• n: The number of apples that Nate picked.
• l: The number of apples that Laura picked.

We know that Laura picked 1/2 as many apples as Nate, so we can write the following equation:

`\sf l = (n )/( 2)`

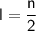
We also know that Nate and Laura picked a total of 90 apples, so we can write the following equation:

`\sf n + l = 90`

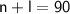
Now we have two independent equations with two unknowns, so we can solve for n and l.

Substituting the first equation into the second equation, we get:

`\sf n + (n)/(2)= 90`

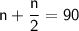
Simplifying the left-hand side, we get:

`\sf (2n+n )/(2 )= 90`

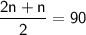
Multiplying both sides of the equation by 2, we get:

`\sf 3n = 90*2`

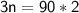
3n = 180

Dividing both sides of the equation by 3, we get:

`\sf (3n)/(3)=(180)/(3)`

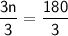
n = 60

Now that we know n, we can find l using the first equation:

`\sf l = (60 )/(2) = 30`

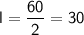
Summary of the solution:

• Equation:
  `\sf n + (n)/(2)= 90`
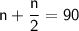
• Nate picked 60 apples.
• Laura picked 30 apples.

`\hrulefill`

For 2nd Question:

Let's use the following variables:

• n = distance Jordan travels
• h = distance Harrison travels

We know that Jordan travels
`(3)/(4)` of a mile longer to school each day than Harrison does, so we can write the following equation:

`\sf n = h + (3)/(4)`

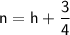
We also know that together they travel
`\sf 5(1)/(4) =(21)/(4)` miles to school, so we can write the following equation:

`\sf n + h = (21)/(4)`

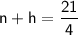
Now we can solve for n and h using the substitution method.

Substituting the first equation into the second equation, we get the following equation:

`\sf h + (3)/(4) + h = (21)/(4)`

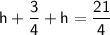
Combining like terms, we get:

`\sf 2h + (3)/(4) = (21)/(4)`

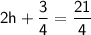
Subtracting
`\sf (3)/(4)` from both sides, we get:

`\sf \sf 2h =(21)/(4)-(3)/(4)`

`\sf 2h = (21-3)/(4)`

`\sf 2h = (18)/(4)`

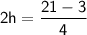
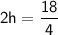
Dividing both sides by 2, we get:

`\sf h=(18)/(4)*(1)/(2)`

`\sf h = (18)/(8)`

`\sf h = (9)/(4)`

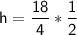
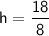
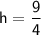
Now that we know the value of h, we can find the value of n by substituting it into the first equation.

`\sf n = h + (3)/(4)`

`\sf n = (9)/(4) + (3)/(4)`

`\sf n = (12)/(4)`

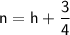
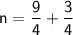
n = 3

In summary:

• Equation:
  `\sf h + (3)/(4) + h = (21)/(4)`
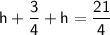
• Jordan travels 3 miles to school.
• Harrison travels
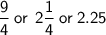  `\sf (9)/(4 )\:or\: \:2(1)/(4) \:or\: 2.25`miles to school.

`\hrulefill`

For 3rd Question:

Sure, I can help you with that.

Let's use the following variables:

• n = cost of Jacket A
• b = cost of Jacket B

We know that Jacket A costs $12 less than Jacket B, so we can write the following equation:

`\sf n = b - 12`

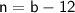
We also know that together the jackets cost $98, so we can write the following equation:

`\sf n + b = 98`

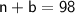
Now we can solve for n and b using the substitution method.

Substituting the first equation into the second equation, we get the following equation:

`\sf (b - 12) + b = 98`

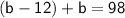
Combining like terms, we get:

`\sf 2b - 12 = 98`

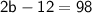
Adding 12 to both sides, we get:

`\sf 2b = 98+12`

`\sf 2b = 110`

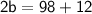
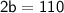
Dividing both sides by 2, we get:

`\sf b =(110)/(2)`

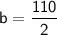
b = 55

Now that we know the value of $b$, we can find the value of $n$ by substituting it into the first equation.

`\sf n = b - 12`

`\sf n = 55 - 12`

`\sf n = 43`

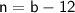
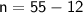
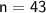
Summary:

• Equation:
  `\sf \sf (b - 12) + b = 98`
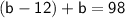
• Jacket A costs $43
• Jacket B costs $55.