Question

HELP! answer and explanation plss

Answer 1

SA = π(3²) + π(3)(5) = (9 + 15)π = 24π cm²

24 should go into the box.

Answer 2

`\sf SA=\boxed{24}\;\pi \; cm^2`

Explanation:

The given formula for the surface area of a cone is:

`\large\boxed{\textsf{S.A.} = \pi r \ell + B}`

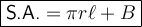
where:

• r is the radius of the base of the cone.
• 
  `\ell` is the slant height of the cone.
• B is the area of the base of the cone.

From observation of the given diagram:

• Radius, r = 3 cm
• Height, h = 4 cm

The slant height (
`\ell`) can be calculated using Pythagoras Theorem:

`\begin{aligned}\ell^2&=r^2+h^2\\\ell^2&=3^2+4^2\\\ell^2&=9+16\\\ell^2&=25\\\ell&=5\end{aligned}`

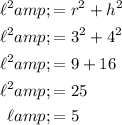
The base of the cone is a circle, so the area of the base can be calculated using the formula for the area of a circle, B = πr², where r is the radius. Therefore:

`\begin{aligned}B&=\pi \cdot 3^2\\B&=9\pi\; \sf cm^2\end{aligned}`

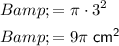
To calculate the total surface area, substitute the values of r,
`\ell` and B into the given formula for the surface area of the cone:

`\begin{aligned}\textsf{S.A.} &= \pi r \ell + B\\\textsf{S.A.} &= \pi \cdot 3 \cdot 5 + 9\pi\\\textsf{S.A.} &= 15\pi + 9\pi\\\textsf{S.A.} &= 24\pi\; \sf cm^2\end{aligned}`

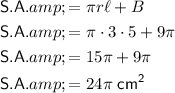
Therefore, the total surface area of the cone is 24π cm².