Question

In ΔXYZ, x = 19.2 meters, y = 21 meters, and z = 19.1 meters. Find the remaining measurements of the triangle, and round your answers to the nearest tenth.

∠X = 57°, ∠Y = 66.5°, ∠Z = 56.5°
∠X = 28.6°, ∠Y = 91.2°, ∠Z = 56.5°
∠X = 28.6°, ∠Y = 91.2°, ∠Z = 60.2°
∠X = 57°, ∠Y = 66.5°, ∠Z = 60.2°



I’m rlly desperate pls ☠️

Answer 1

A) ∠X = 57°, ∠Y = 66.5°, ∠Z = 56.5°

Explanation:

To find the interior angles of triangle XYZ, first use the cosine rule to find one angle.

`\boxed{\begin{minipage}{6 cm}\underline{Cosine Rule} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}`

Given sides lengths:

• x = 19.2 meters
• y = 21 meters
• z = 19.1 meters

Use the cosine rule to find the measure of angle Z:

`\begin{aligned}z^2&=x^2+y^2-2xy \cos Z\\\\19.1^2&=19.2^2+21^2-2(19.2)(21) \cos Z\\\\19.1^2-19.2^2-21^2&=-2(19.2)(21) \cos Z\\\\(19.1^2-19.2^2-21^2)/(-2(19.2)(21))&= \cos Z\\\\Z&=\cos^(-1)\left((19.1^2-19.2^2-21^2)/(-2(19.2)(21))\right)\\\\Z&=\cos^(-1)\left((-444.83)/(-806.4)\right)\\\\Z&=\cos^(-1)\left((44483)/(80640)\right)\\\\Z&=56.5^(\circ)\; \sf (nearest\;tenth)\end{aligned}`

Now, use the sine rule to find the measures of angles X and Y.

`\boxed{\begin{minipage}{7.6 cm}\underline{Sine Rule} \\\\$(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

Substitute the given values of x, y and z, and the found (exact) measure of angle Z into the sine rule formula:

`(\sin X)/(x)=(\sin Y)/(y)=(\sin Z)/(z)`

`(\sin X)/(19.2)=(\sin Y)/(21)=(\sin \left(\cos^(-1)\left((44483)/(80640)\right)\right))/(19.1)`

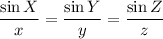
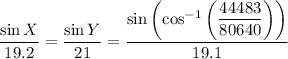
Solving for X:

`X=\sin^(-1)\left((19.2\sin \left(\cos^(-1)\left((44483)/(80640)\right)\right))/(19.1)\right)=56.97780...^(\circ)=57^(\circ)`

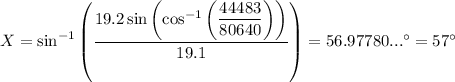
Solving for Y:

`Y=\sin^(-1)\left((21\sin \left(\cos^(-1)\left((44483)/(80640)\right)\right))/(19.1)\right)=66.500725...^(\circ)=66.5^(\circ)`

Therefore, the interior angles of triangle XYZ are:

• m∠X = 57°
• m∠Y = 66.5°
• m∠Z = 56.5°