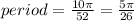Question

Below is the graph of a trigonometric function. It intersects its midline at (-10.7,-3) and again at (-5.5,-3)

What is the period of the function? Give an exact value.

Answer 1

Explanation:

The period of the function is how long 1 cycle is. On the graph, we are only given half of one cycle, which is 5.2 units long; that means that the whole cycle is that value times 2 or 10.4 units. The period formula is

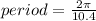`period=(2\pi)/(10.4)` which is the same thing as

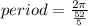`period=(2\pi)/((52)/(5) )`which gives us

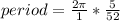`period=(2\pi)/(1)*(5)/(52)` and

`period=(10\pi)/(52)=(5\pi)/(26)`