Question

A deposit of 100 is invested in an account for 10 years. It earns a constant force of interest of 4% in the first 3 years, an annual effective rate of discount of 4% during the next 5 years, and an annual simple interest rate of 4% during the remaining years Determine the annual effective interest rate earned over the 10 -year period that results in the same ending account balance as these given rates.

Answer 1

To find the annual effective interest rate over 10 years that results in the same ending account balance, calculate the future value of the initial deposit using the given rates. The annual effective interest rate is approximately 1.63%.

Step-by-step explanation:

To determine the annual effective interest rate earned over the 10-year period that results in the same ending account balance, we need to calculate the future value of the initial deposit using the given rates. Here's how:

1. Calculate the future value of the initial deposit for the first 3 years with a constant force of interest of 4% annually. Using the formula: Future Value = Initial Deposit * (1 + Interest Rate) ^ Number of Years. So, Future Value =
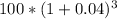   `100 * (1 + 0.04) ^ 3` = $112.24.
2. Calculate the future value of the remaining balance ($112.24) for the next 5 years with an annual effective rate of discount of 4%. Using the formula:
3. Future Value = Initial Deposit / (1 + Interest Rate) ^ Number of Years. So, Future Value =
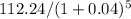   `112.24 / (1 + 0.04) ^ 5` = $91.49.
4. Calculate the future value of $91.49 for the remaining 2 years with an annual simple interest rate of 4%. Using the formula: Future Value = Initial Deposit * (1 + Interest Rate * Number of Years). So, Future Value =
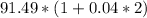   `91.49 * (1 + 0.04 * 2)` = $94.77.

Now, we have the future value of the initial deposit after 10 years, which is $94.77. To find the annual effective interest rate that produces the same ending balance, we can use the formula for future value of an investment:

Future Value = Initial Deposit * (1 + Annual Effective Interest Rate) ^ Number of Years. Rearranging the formula to solve for the Annual Effective Interest Rate: Annual Effective Interest Rate = (Future Value / Initial Deposit) ^ (1 / Number of Years) - 1.

Substituting the values: Annual Effective Interest Rate

`= ($94.77 / $100) ^ (1 / 10) - 1`

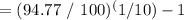
= 0.0163, which is approximately 1.63%.