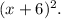Question

X is an integer. Prove that ,35+(3x+1)^(2)-2x(4x-3), is a square number.

Answer 1

To prove that 35+(3x+1)^(2)-2x(4x-3) is a square number, we can simplify the expression and factor it to show that it is equivalent to (x + 6)^2.

Step-by-step explanation:

To prove that 35+(3x+1)^(2)-2x(4x-3) is a square number, we need to show that it can be written in the form a^2 for some integer a. Let's simplify the expression step by step:

1. Expand the square: (3x+1)^(2) = 9x^2 + 6x + 1.
2. Simplify the product term: -2x(4x-3) = -8x^2 + 6x.
3. Combine like terms: 35 + 9x^2 + 6x + 1 - 8x^2 + 6x = x^2 + 12x + 36.
4. Factor the trinomial: x^2 + 12x + 36 = (x + 6)^2.

Therefore, the expression 35+(3x+1)^(2)-2x(4x-3) is equivalent to the square of the binomial x + 6. This confirms that it is a square number.

Answer 2

To prove the given expression is a square number, we can rewrite it as a perfect square which comes as
`(x+6)^2.`

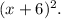
Step-by-step explanation:

To prove that the expression
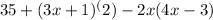`35 + (3x+1)^(2) - 2x(4x-3)` is a square number, we need to show that it can be expressed in the form of k^2 where k is an integer.

Let's simplify the expression step by step:

1. Expand the square term:
   `(3x+1)^(2) = (3x+1)(3x+1) = 9x^2 + 6x +1`
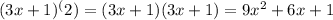
2. Distribute the second term:
   `2x(4x-3) = 8x^2 -6x`
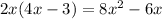
3. Combine like terms:
   `35 + 9x^2 + 6x +1 -8x^2 +6x = 36 + x^2 + 12x`

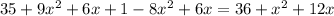
Now, we can rewrite the expression as a perfect square:
`36 + x^2 + 12x = (x+6)^2`

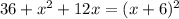
Therefore, the expression
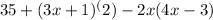`35 + (3x+1)^(2) - 2x(4x-3)` is a square number because it can be expressed as
`(x+6)^2.`