Question

Use completing the square to rewrite the equation: x^(2)+4x-5=0

Answer 1

`\huge\boxed{\sf x = -5,1}`

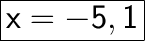
Explanation:

Given equation:

x² + 4x - 5 = 0

Since we are following completing square method, move the constant to the opposite side.

• Add 5 to both sides.

x² + 4x = 5

Now, we can write the above equation as:

(x)² + 2(x)(2) = 5

Add (2)² to both sides, so that the square can be completed.

(x)² + 2(x)(2) + (2)² = 5 + (2)²

Using formula: a² + 2ab + b² = (a + b)²

So, the equation becomes,

(x + 2)² = 5 + 4

(x + 2)² = 9

• Take square root on both sides.

√(x + 2)² = ±√9

x + 2 = ±3

Either,

x + 2 = 3 OR x + 2 = -3

x = 3 - 2 OR x = -3 - 2

x = 1 OR x = -5

`\rule[225]{225}{2}`