Question

The graph shows that f(x)=3* is translated

horizontally and vertically to create the function
g(x)=3*-+k.
10)
g(x)
What is the value of h?
O-2
0-1
01
02

Answer 1

h = 2

Explanation:

Given graphed functions:

`f(x)=3^x`

`g(x)=3^(x-h)+k`

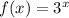
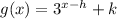
From inspection of the given graph (attached), function f(x) has been translated 2 units right and 2 units up to create function g(x).

When translating a function n units to the right, we subtract n from the x-variable of the function.

When translating a function n units up, we add n to the function.

Therefore, function f(x) translated 2 units to the right and 2 units up gives:

`g(x)=f(x-2)+2\\\\g(x)=3^(x-2)+2`

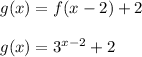
Compare the found function for g(x) with the given function for g(x):

`3^(x-h)+k=3^(x-2)+2`

Therefore, the value of h is 2 (and the value of k is 2).