Answer:
Approximately
 .
.
Step-by-step explanation:
The
 -coordinate of the center of mass of this system is the average
-coordinate of the center of mass of this system is the average
 -coordinate of the spheres, weighted according to the mass of each sphere.
-coordinate of the spheres, weighted according to the mass of each sphere.
For example, if a sphere of mass
 is at
is at
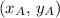 , a sphere of mass
, a sphere of mass
 is at
is at
 , a sphere of mass
, a sphere of mass
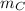 is at
is at
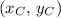 , and a sphere of mass
, and a sphere of mass
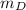 is at
is at
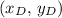 , the
, the
 -coordinate of the center of mass would be at:
-coordinate of the center of mass would be at:
![\begin{aligned} (\sum\limits_(j=1)^(n) \left[m_(j)\, x_(j)\right])/(\sum\limits_(j=1)^(n) \left[m_(j)\right]) = (m_(A)\, x_(A) + m_(B)\, x_(B) + m_(C) \, x_(C) + m_(D)\, x_(D))/(m_(A) + m_(B) + m_(C) + m_(D))\end{aligned}](https://img.qammunity.org/2024/formulas/physics/high-school/msblsmms0u2bfanrswo834hwmmtky87tca.png) .
.
Similarly, the
 -coordinate of the center of mass would be the weighted average of the
-coordinate of the center of mass would be the weighted average of the
 -coordinates of the spheres:
-coordinates of the spheres:
![\begin{aligned} (\sum\limits_(j=1)^(n) \left[m_(j)\, y_(j)\right])/(\sum\limits_(j=1)^(n) \left[m_(j)\right]) = (m_(A)\, y_(A) + m_(B)\, y_(B) + m_(C) \, y_(C) + m_(D)\, y_(D))/(m_(A) + m_(B) + m_(C) + m_(D))\end{aligned}](https://img.qammunity.org/2024/formulas/physics/high-school/kwlaokxe26ds1viauzgr0bc6efjrnfhghs.png) .
.
In this question, the mass of each sphere has been given. The position of sphere
 ,
,
 , and
, and
 are also given.
are also given.
The goal is to find the coordinates
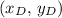 of sphere
of sphere
 such that the center of mass is at the origin
such that the center of mass is at the origin
 . To do so, set the
. To do so, set the
 - and
- and
 -coordinates of the center of mass to
-coordinates of the center of mass to
 and obtain two equations. Solve these two equations to obtain
and obtain two equations. Solve these two equations to obtain
 and
and
 .
.
Given the mass and position of the other spheres, the expression for the
 -coordinate of the center of mass would be:
-coordinate of the center of mass would be:
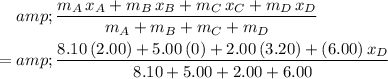 .
.
Set this expression to
 (
(
 -coordinate of the origin) and solve for the
-coordinate of the origin) and solve for the
 :
:
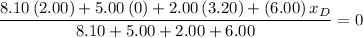 .
.
Note that the denominator can be eliminated:
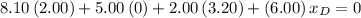 .
.
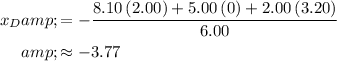 .
.
In other words, the
 -coordinate of sphere
-coordinate of sphere
 should be approximately
should be approximately
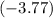 meters.
meters.
Similarly, set the expression for the
 -coordinate of the center of mass to
-coordinate of the center of mass to
 and solve for
and solve for
 :
:
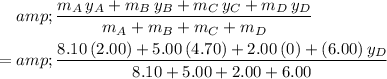 .
.
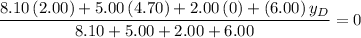 .
.
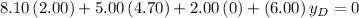 .
.
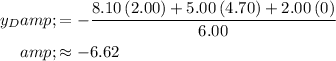 .
.
In other words, the
 -coordinate of sphere
-coordinate of sphere
 should be approximately
should be approximately
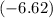 meters.
meters.
Therefore, the position of this
 sphere should be approximately
sphere should be approximately
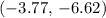 meters.
meters.