Question

The difference between the Cl compounded annually and the SI on a certain sum for 3 years at 10% p.a. is 62. Find the sum.​

Answer 1

principal amount or sum is 2000.

Explanation:

Given:

• R = 10% p.a.
• T = 3 years
• CI - SI = 62

The formula for compound interest is:

`\sf CI = P\left(1 + (R)/(100)\right)^T -P`

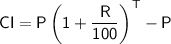
Where:

• CI = compound interest
• P = principal amount
• R = interest rate
• T = time in years

The formula for simple interest is:

`\sf SI =( P*R*T)/(100)`

Where:

• SI = simple interest
• P = principal amount
• R = interest rate
• T = time in years

We can use the difference between the compound interest and simple interest to solve for the principal amount as follows:

CI - SI = 62

`\sf P\left(1 + (R)/(100)\right)^T -P- ( P*R*T)/(100) = 62`

Taking common P

`\sf P\left[\left(1 + (R)/(100)\right)^T - 1 - (RT)/(100)\right] = 62`

Substituting value

`\sf P\left[\left(1 + (10)/(100)\right)^(3) - 1 - (10*3)/(100)\right] = 62`

`\sf P\left[ (1.1)^3-1 -0.3\right]= 62`

`\sf P[1.331 - 1 - 0.3] = 62`

`\sf P[0.031]= 62`

`\sf P =( 62)/(0.031)= 2000`

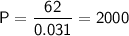
Therefore, the principal amount or sum is 2000.