Question

Solve: sec b cosec b=2 cosec b

Answer 1

b = 60° or 300°

Explanation:

We can solve the equation
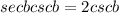`sec b csc b=2 csc b` in terms of sin and cos as follows:

We can write sec b and csc b in terms of sin and cos:

`\sf sec \:b = (1)/(\:cos\: b)`

`\sf csc b = (1)/(sin \:b)`

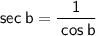
Substituting these expressions into the equation, we get:

`\sf (1)/(cos b) \cdot (1)/(sin b) = 2 \cdot (1)/(sin b)`

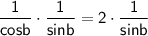
Multiplying both sides of the equation by sin b cos b, we get:

`\sf 1 = 2\cdot (cosb\cdot sinb)/(sinb)`

`\boxed{\sf (sin b)/(sinb)=1}`

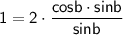
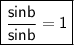
so,

`\sf 1 = 2\: cos b`

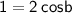
Dividing both sides of the equation by 2, we get:

`\sf (1)/(2) =cos b`

`\sf cos 60^\circ = cos b`

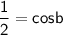
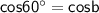
Since cos is positive in 1st and 4th quadrant, so

`\sf cos 60^\circ \:\:or\:\:cos(360^\circ-60^\circ)= cos b`

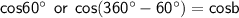
Therefore, the solutions to the equation
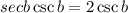`sec b \csc b=2 \csc b` for b is 60° or 300°