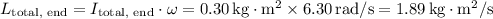(a) The angular momentum of the system when the stick is pivoted about an axis perpendicular to the table and passing through its center is
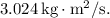
(b) The angular momentum of the system when the stick is pivoted about an axis perpendicular to it and at the end furthest from the attached mass is
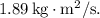
(a) When the stick is pivoted about an axis perpendicular to the table and passing through its center:
The formula for angular momentum is
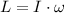 , where L is the angular momentum, I is the moment of inertia, and
, where L is the angular momentum, I is the moment of inertia, and
 is the angular speed.
is the angular speed.
First, let's calculate the moment of inertia of the system about the center when pivoted from its center.
The moment of inertia I for a point mass rotating about an axis at a distance r is
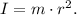
Given:
Mass of the stick
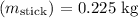
Length of the stick
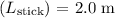
Distance of the attached mass from the center

Angular speed

First, calculate the moment of inertia of the stick about its center:
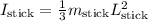 (for a thin rod rotating about its center)
(for a thin rod rotating about its center)
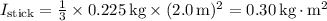
The moment of inertia of the attached mass about the center is
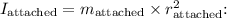
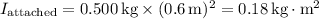
The total moment of inertia about the center is the sum of the moments of inertia of the stick and the attached mass:
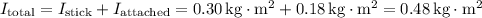
Now, calculate the angular momentum using the formula
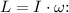
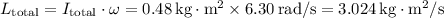
(b) When the stick is pivoted about an axis perpendicular to it and at the end furthest from the attached mass:
In this case, the moment of inertia will be different because the pivot point changes.
For a thin rod rotating about one end, the moment of inertia
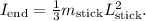
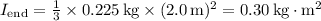
The total moment of inertia about this pivot point is only considering the stick itself, as the point mass is at the pivot:
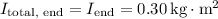
Using the same angular speed, calculate the angular momentum: