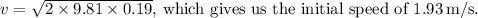The initial speed of 1.93m/s.
The initial speed of water flowing out of a hole in a container can be calculated using Torricelli's Law, which is derived from Bernoulli's Principle and the conservation of energy. The formula for the initial velocity
 of the efflux is:
of the efflux is:
![\[ v = √(2gh) \]](https://img.qammunity.org/2024/formulas/physics/high-school/utrb5773abfhh03l0f7oyvm5cdvk85tzik.png)
where:
-
 is the acceleration due to gravity
is the acceleration due to gravity
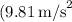 on Earth),
on Earth),
-
 is the height of the water column above the hole in meters.
is the height of the water column above the hole in meters.
In this case, the container is 114 cm deep and the hole is 95.0 cm from the top, which means the height
 of the water column above the hole is:
of the water column above the hole is:
![\[ h = 114 \, \text{cm} - 95.0 \, \text{cm} = 19.0 \, \text{cm} = 0.19 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/spa75rsa199d1nvqy999wnio8qgs3p4tmt.png)
Now we can calculate the initial velocity of the water flowing out:
![\[ v = \sqrt{2 * 9.81 \, \text{m/s}^2 * 0.19 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/b9qlflhtkz621xxlwjgsfhk3vr8o3kpfzt.png)
Let's do the calculation.
The initial speed at which the water will flow from the hole is approximately
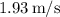 . Here's how we got the result:
. Here's how we got the result:
1. We first converted the height of the water column above the hole into meters:
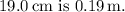
2. Then we applied Torricelli's Law using the formula
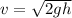 , with
, with
 being the acceleration due to gravity
being the acceleration due to gravity
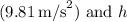 the height of the water above the hole.
the height of the water above the hole.
3. The calculation yields