Question

A 8.49-g geological sample, containing the mineral Boulangerite (Pb5Sb4S11) as the only lead-bearing compound, is subjected to chemical treatment in which the lead is quantitatively recovered as solid PbCl2. The mass of PbCl2 obtained is 3.92 g.

What was the percentage (by mass) of Pb5Sb4S11 in the sample?

Answer 1

The percentage (by mass) of
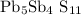`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` in the sample is approximately 62.32%.

To find the percentage (by mass) of
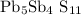`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` in the sample, we can start by determining the molar mass of
`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$`.

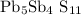The molar mass of
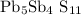`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` can be calculated by adding the atomic masses of each element in the compound:

• Atomic mass of Pb (lead) = 207.2 g/mol
• Atomic mass of Sb (antimony) = 121.76 g/mol
• Atomic mass of S (sulfur) = 32.06 g/mol

Molar mass of
`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$`:

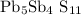`\[5 * \text{Atomic mass of Pb} + 4 * \text{Atomic mass of Sb} + 11 * \text{Atomic mass of S}\]`

`\[= 5 * 207.2 \, \text{g/mol} + 4 * 121.76 \, \text{g/mol} + 11 * 32.06 \, \text{g/mol}\]`

`\[= 1036 + 487.04 + 352.66\]`

`\[= 1875.7 \, \text{g/mol}\]`

Next, we'll find the number of moles of
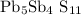`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` present in the 8.49 g sample:

Number of moles =
`\frac{\text{Mass}}{\text{Molar mass}}`

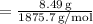
Number of moles
`= \frac{8.49 \, \text{g}}{1875.7 \, \text{g/mol}}`

Number of moles ≈
`0.00452 \, \text{mol}`

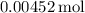
Since the lead in
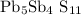`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` was recovered as
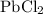`$\mathrm{PbCl}_2$`, we need to find the moles of lead in
`$\mathrm{PbCl}_2$`.

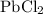The molar mass of
`$\mathrm{PbCl}_2$`:

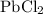`\[ \text{Atomic mass of Pb} + 2 * \text{Atomic mass of Cl} = 207.2 \, \text{g/mol} + 2 * 35.45 \, \text{g/mol} = 278.1 \, \text{g/mol}\]`

Number of moles of
`$\mathrm{PbCl}_2$`:

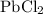`\[ \text{Number of moles} = \frac{\text{Mass}}{\text{Molar mass}} = \frac{3.92 \, \text{g}}{278.1 \, \text{g/mol}} = 0.0141 \, \text{mol}\]`

Since 1 mol of
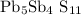`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` contains 5 moles of lead (Pb), we can calculate the moles of
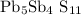`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` corresponding to the moles of lead obtained:

`\[ \text{Moles of } \mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11) = \frac{\text{Number of moles of PbCl}_2}{5} = \frac{0.0141 \, \text{mol}}{5} = 0.00282 \, \text{mol}\]`

Finally, let's calculate the mass of
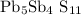`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` in the sample:

`\[ \text{Mass of } \mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11) = \text{Number of moles} * \text{Molar mass}\]`

`\[ \text{Mass of } \mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11) = 0.00282 \, \text{mol} * 1875.7 \, \text{g/mol} = 5.29 \, \text{g}\]`

Now, the percentage (by mass) of
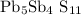`$\mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)$` in the sample is:

`\[ \text{Percentage} = \frac{\text{Mass of } \mathrm{Pb}_5 \mathrm{Sb}_4 \mathrm{~S}_(11)}{\text{Total mass of sample}} * 100\]`

`\[ \text{Percentage} = \frac{5.29 \, \text{g}}{8.49 \, \text{g}} * 100 = 62.32\%\]`

Therefore, The answer is approximately 62.32%.

Answer 2

The percentage of the lead is 46% in the sample.

What is percentage by mass of a chemical specie in a sample?

The percentage by mass of a chemical species in a sample is a measure of the mass contribution of that particular species to the total mass of the sample.

Percentage by mass is commonly used in chemistry to express the composition of mixtures, the concentration of solutions, or the makeup of compounds in a sample.

We have that;

Mass of the Boulangerite - 8.49-g

Mass of the recovered lead II chloride - 3.92 g

Mass percent of the
`Pb_5Sb_4S_{11` = 3.92 g/8.49 g * 100/1

= 46%