The weight percent of each component in the impure
 sample is as follows:
sample is as follows:
-
 : 80.93%
: 80.93%
-
 : 5.94%
: 5.94%
-
 : 13.13%
: 13.13%
To find the weight percent of each component in the impure vanadyl sulfate sample, we will need to follow these steps:
1. Calculate the moles of
 ion in the original 50.0 mL solution using the concentration obtained from spectrophotometric analysis.
ion in the original 50.0 mL solution using the concentration obtained from spectrophotometric analysis.
2. Calculate the mass of pure
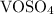 that corresponds to the moles of
that corresponds to the moles of
 ion.
ion.
3. Calculate the moles of
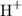 released from the cation-exchange column, which is equal to the moles of
released from the cation-exchange column, which is equal to the moles of
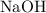 used in the titration.
used in the titration.
4. Calculate the mass of
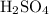 that corresponds to the moles of
that corresponds to the moles of
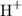 ions.
ions.
5. Subtract the mass of
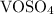 and
and
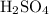 from the initial mass of the impure sample to find the mass of
from the initial mass of the impure sample to find the mass of
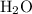 .
.
6. Calculate the weight percent of each component.
Let's start with step 1:
1. Calculate the moles of
 ion in the original 50.0 mL solution:
ion in the original 50.0 mL solution:
The concentration of
 is given as 0.0243 M, which means there are 0.0243 moles of
is given as 0.0243 M, which means there are 0.0243 moles of
 per liter of solution. Since we have 50.0 mL, we need to adjust for the volume:
per liter of solution. Since we have 50.0 mL, we need to adjust for the volume:
![\[ \text{Moles of } \text{VO}^(2+) = 0.0243 \, \text{M} * \frac{50.0 \, \text{mL}}{1000 \, \text{mL/L}} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/i4lwrtt67n6va5kgtjvbvg4fbl2ykvy7c1.png)
Let's do this calculation.
The moles of
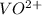 ion in the original 50.0 mL solution are 0.001215 moles.
ion in the original 50.0 mL solution are 0.001215 moles.
2. Calculate the mass of pure
 that corresponds to the moles of
that corresponds to the moles of
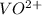 ion:
ion:
To find the mass of
 , we multiply the moles of
, we multiply the moles of
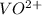 by the formula weight (FM) of
by the formula weight (FM) of
 .
.
![\[ \text{Mass of } VOSO_4 = \text{moles of } VO^(2+) * \text{FM of } VOSO_4 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/5na3lajlayv6bxpgsf9r7i3aqtvpwvlhdv.png)
The formula weight (FM) of
 is given as 163.00 g/mol.
is given as 163.00 g/mol.
![\[ \text{Mass of } VOSO_4 = 0.001215 \text{ mol} * 163.00 \text{ g/mol} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/zgtqq5mc3tlsf2gz3agkbzagm0flxezfxs.png)
Let's calculate this.
The mass of pure
 that corresponds to the moles of
that corresponds to the moles of
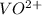 ion is 0.1980 g.
ion is 0.1980 g.
3. Calculate the moles of
 released from the cation-exchange column, which is equal to the moles of
released from the cation-exchange column, which is equal to the moles of
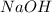 used in the titration:
used in the titration:
![\[ \text{Moles of } NaOH = \text{Volume of } NaOH * \text{Molarity of } NaOH \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/v3tdh5usrf7j5usxp5yl2ykg4av7nu1d7s.png)
![\[ \text{Moles of } NaOH = 13.03 \text{ mL} * \frac{0.02274 \text{ mol}}{1000 \text{ mL}} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/mdvoy3d7k7gsmqdo6a6pw2mwl97wr7ffjv.png)
Let's calculate the moles of
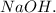
The moles of
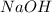 used in the titration (and thus the moles of
used in the titration (and thus the moles of
 released) are 0.0002963 moles.
released) are 0.0002963 moles.
4. Calculate the mass of
 that corresponds to the moles of \( H^+ \) ions. Each mole of
that corresponds to the moles of \( H^+ \) ions. Each mole of
 releases 2 moles of \( H^+ \), so we need to halve the moles of
releases 2 moles of \( H^+ \), so we need to halve the moles of
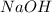 to find the moles of
to find the moles of
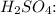
![\[ \text{Moles of } H_2SO_4 = \frac{\text{Moles of } NaOH}{2} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/vfdcj6pfga085bz2pqi1r1tyikdkcvc2lc.png)
Then, we calculate the mass:
![\[ \text{Mass of } H_2SO_4 = \text{Moles of } H_2SO_4 * \text{FM of } H_2SO_4 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/4gbpsqlqw4dmlvu06qatl0d6fahcc53q4s.png)
The formula weight (FM) of
 is given as 98.08 g/mol.
is given as 98.08 g/mol.
Let's perform these calculations.
The moles of
 are 0.0001481 moles, and the corresponding mass of
are 0.0001481 moles, and the corresponding mass of
 is approximately 0.01453 g.
is approximately 0.01453 g.
5. Subtract the mass of
 and
and
 from the initial mass of the impure sample to find the mass of
from the initial mass of the impure sample to find the mass of

![\[ \text{Mass of impure } VOSO_4 \text{ sample} - (\text{Mass of } VOSO_4 + \text{Mass of } H_2SO_4) = \text{Mass of } H_2O \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/2jnubm57mbz1r6o1pziczjbuql0vsdwgvp.png)
The initial mass of the impure
 sample is given as 0.2447 g.
sample is given as 0.2447 g.
![\[ \text{Mass of } H_2O = 0.2447 \text{ g} - (0.1980 \text{ g} + 0.01453 \text{ g}) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/rkp1aqadbi144wnn4pact9hbnu9zbzn5g9.png)
Let's calculate the mass of
 .
.
The mass of
 in the impure
in the impure
 sample is approximately 0.03212 g.
sample is approximately 0.03212 g.
6. Calculate the weight percent of each component:
![\[ \text{Weight percent of } VOSO_4 = \left( \frac{\text{Mass of } VOSO_4}{\text{Mass of impure sample}} \right) * 100 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/qs3djc1rncbiy2qs6obn5itzo7h03hy5u6.png)
![\[ \text{Weight percent of } H_2SO_4 = \left( \frac{\text{Mass of } H_2SO_4}{\text{Mass of impure sample}} \right) * 100 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/t5uj3rrbex35x2h3fujz8fcp1x5z98o2b7.png)
![\[ \text{Weight percent of } H_2O = \left( \frac{\text{Mass of } H_2O}{\text{Mass of impure sample}} \right) * 100 \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/g3as0fglwqcuyzpyflj0l9jckd3ylx2pna.png)
The weight percent of each component in the impure
 sample is as follows:
sample is as follows:
-
 : 80.93%
: 80.93%
-
 : 5.94%
: 5.94%
-
 : 13.13%
: 13.13%