Question

What is the escape velocity (in km/s) at the Schwarzschild radius of a 6.22 Msun black hole?

Answer 1

The escape velocity would be equal to the speed of light.

c (speed of light) = 299,792,458 m/s or 299,792.458 km/s

Step-by-step explanation:

The escape velocity at the of a black hole refers to the minimum velocity an object must attain to break free from the gravitational pull of the black hole at that specific distance. The Schwarzschild radius, often denoted as 'r_s', is a characteristic radius associated with a non-rotating black hole. It is given by the formula:

`\boxed{\left\begin{array}{ccc}\text{\underline{Schwarzschild Radius:}}\\\\r_s=(2GM)/(c^2)\\\\\text{Where:}\\\bullet \ r_s \ \text{is the radius of the event horizon of a black hole}\\\bullet \ G \ \text{is the gravitational constant}\ (6.67 * 10^(-11) \ (Nm^2)/(kg^2) ) \\\bullet \ M \ \text{is the mass of the black hole}\\\bullet \ c \ \text{is the speed of light} \ (3.00 * 10^8 \ m/s)\end{array}\right }`

The event horizon can be conceptualized as the boundary at which the escape velocity equals the speed of light.

The formula for escape velocity (v_e) from the surface of a celestial body is given by:

`\boxed{\left\begin{array}{ccc}\text{\underline{Escape Velocity:}}\\\\v_e=\sqrt{(2GM)/(r) }\\\\ \text{Where:}\\ \bullet \ v_e \ \text{is the escape velocity (in m/s)}\\ \bullet \ G \ \text{is the gravitational constant}\ (6.67 * 10^(-11) \ (Nm^2)/(kg^2) ) \\ \bullet \ M \ \text{is the mass of the celestial body} \\ \bullet \ r \ \text{is the distance from the center of the celestial body} \end{array}\right}`

In the context of your question, the Schwarzschild radius (r_s) is the distance from the center of the black hole where the escape velocity becomes equal to the speed of light (c). This means that any object attempting to escape from within the Schwarzschild radius would need to reach the speed of light, which is not possible according to our current understanding of physics.

`\hrulefill`

Let's prove this mathematically:

Using the formula for escape velocity, r = r_s. Lets make this substitution:

`v_e=\sqrt{(2GM)/(r) }; \ r_s=(2GM)/(c^2); \ \text{Where} \ r = r_s\\\\\\\\\Longrightarrow v_e=\sqrt{(2GM)/(\Big((2GM)/(c^2)\Big)) }\\\\\\\\\Longrightarrow v_e=\sqrt{(2GMc^2)/(2GM) } \\\\\\\\\Longrightarrow v_e=√(c^2) \\\\\\\\\therefore \boxed{\boxed{v_e = c}}`

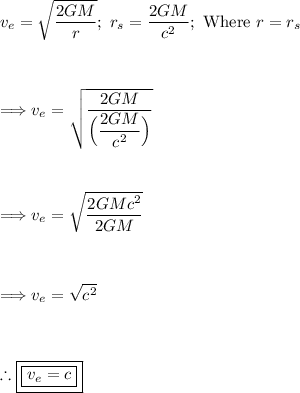
Thus, we have proven that the escape velocity is equal to that of the speed of light.