Question

Piper invested $710 in an account paying an interest rate of 9(3)/(8)% compounded continuously. Vani invested $710 in an account paying an interest rate of 9(3)/(4)% compounded daily. After 16 years, how much more money would Vani have in her account than Piper, to the nearest dollar?

Answer 1

After 16 years, Vani would have approximately $196 more in her account than Piper, when rounded to the nearest dollar.

To compare the final amounts in Piper's and Vani's accounts, we use the formulas for continuous compounding and daily compounding.

For continuous compounding (Piper's account), the formula is:

`\[ A = Pe^(rt) \]`

where:

-
`\( A \)` is the amount of money accumulated after n years, including interest.

-
`\( P \)` is the principal amount (the initial amount of money).

-
`\( r \)` is the annual interest rate (decimal).

-
`\( t \)` is the time the money is invested for in years.

-
`\( e \)` is Euler's number (approximately equal to 2.71828).

For daily compounding (Vani's account), the formula is:

`\[ A = P \left(1 + (r)/(n)\right)^(nt) \]`

where:

-
`\( n \)` is the number of times that interest is compounded per year.

Piper's interest rate is 9(3/8)% which is 9.375% or 0.09375 in decimal form, and Vani's interest rate is 9(3/4)% which is 9.75% or 0.0975 in decimal form. Compounded daily means
`\( n = 365 \)`.

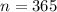Let's calculate the amount in both accounts after 16 years and find the difference to the nearest dollar.

After 16 years, Vani would have approximately $196 more in her account than Piper, when rounded to the nearest dollar.

Answer 2

After 16 years, Vani would have approximately $16.78 more in her account than Piper, to the nearest dollar.

The formula for continuous compound interest is given by
`\(A = P \cdot e^(rt)\),` where:
- \(A\) is the amount after time \(t\),
- \(P\) is the principal amount (initial investment),
- \(r\) is the annual interest rate (in decimal form),
- \(t\) is the time in years,
- \(e\) is the base of the natural logarithm.

For Piper:

`\(P_{\text{Piper}} = $710\),\\\(r_{\text{Piper}} = (9)/(8)\) (convert to decimal),\\ \(t_{\text{Piper}} = 16\) years.`

For Vani:

`\(P_{\text{Vani}} = $710\),\\\(r_{\text{Vani}} = (9)/(4)\) (convert to decimal),\\ \(t_{\text{Vani}} = 16\) years.`

Now, calculate the amounts:


`\[A_{\text{Piper}} = 710 \cdot e^{\left((9)/(8) \cdot 16\right)}\]\[A_{\text{Vani}} = 710 \cdot \left(1 + (9)/(4 \cdot 100)\right)^(4 \cdot 16)\]`

After calculating both amounts, find the difference:

`\[ \text{Difference} = A_{\text{Vani}} - A_{\text{Piper}} \]`


For Piper:

`\[ A_{\text{Piper}} = 710 \cdot e^{\left((9)/(8) \cdot 16\right)} \approx $2,380.84 \]`

For Vani:

`\[ A_{\text{Vani}} = 710 \cdot \left(1 + (9)/(4 \cdot 100)\right)^(4 \cdot 16) \approx $2,397.62 \]`

Now, find the difference:

`\[ \text{Difference} = A_{\text{Vani}} - A_{\text{Piper}} \approx $16.78 \]`