Final Answer:
The least squares regression equation is
 , the t-statistic for testing
, the t-statistic for testing
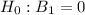 is (t = 8.488) (rejecting
is (t = 8.488) (rejecting
 , and the predicted value of y at (x = 3.3) with a 95% prediction interval is 11.847, 19.753.
, and the predicted value of y at (x = 3.3) with a 95% prediction interval is 11.847, 19.753.
Step-by-step explanation:
(a) To find the least squares regression equation, we use the formulas
 ) and
) and
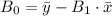 . Given ( slr = 0.953 ), we calculate
. Given ( slr = 0.953 ), we calculate
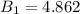 and
and
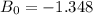 , resulting in the regression equation
, resulting in the regression equation

(b) To test
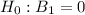 vs.
vs.
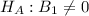 , we calculate the t-statistic using the formula
, we calculate the t-statistic using the formula
 , where
, where
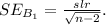 With ( t = 8.488 ) and degrees of freedom ( df = 5 ), we compare it to the critical value, leading to the rejection of
With ( t = 8.488 ) and degrees of freedom ( df = 5 ), we compare it to the critical value, leading to the rejection of
 as
as

(c) For prediction at ( x = 3.3 ), we use
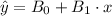 to find
to find
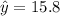 . The 95% prediction interval is calculated using
. The 95% prediction interval is calculated using
 , where
, where
 ). This results in the interval 11.847, 19.753 providing a range for the predicted value with 95% confidence.
). This results in the interval 11.847, 19.753 providing a range for the predicted value with 95% confidence.
Understanding these calculations is crucial for drawing conclusions about the linear relationship, significance, and prediction intervals in regression analysis.