We have proven that if
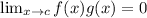 under the given conditions.
under the given conditions.
To prove the statement
![\lim _(x \rightarrow c)[f(x) g(x)]=0](https://img.qammunity.org/2024/formulas/mathematics/high-school/3wrddnpmkbvqks2t67a83nvqu12oc4feve.png) under the given conditions,
under the given conditions,
we will use the Squeeze Theorem.
The Squeeze Theorem states that if
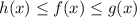 for all x in some open interval containing c, except possibly at c itself, and:
for all x in some open interval containing c, except possibly at c itself, and:
If
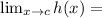
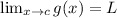
then,
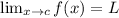 .
.
Given that
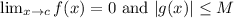 for some fixed number M, we can set up the following inequalities:
for some fixed number M, we can set up the following inequalities:
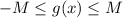
Multiply both sides of the above inequality equation by f(x):

Now, take the limit as x approaches c for each part:
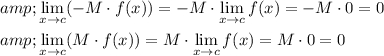
By the Squeeze Theorem, since
 and both the lower and upper bounds approach 0 as x approaches c, it follows that:
and both the lower and upper bounds approach 0 as x approaches c, it follows that:
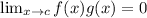
Complete Question: