Question

Find the area of the region enclosed by the graphs of the equations

=, =8, =3

by partitioning (integrating with respect to) the -
axis.

(Use symbolic notation and fractions where needed.)

Answer 1

`A = (63)/(2) \ \text{or} \ 31.5 \ \text{units}^2`

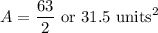
Explanation:

To find the area of the region enclosed by the graphs of the equations y = x, y = 8x, and x = 3, we need to integrate with respect to x. The first step is to visualize the region formed by these equations (refer to the attached photo).

These equations form a triangular region bounded by the lines y = x, y = 8x, and x = 3. To find the area of this region, we need to determine the limits of integration for the variable x.

So, the region is bounded by x = 0 on the left, x = 3 on the right, and y = x and y = 8x as the upper and lower boundaries, respectively.

To find the area using integration, we'll integrate the difference between the upper and lower curves with respect to x, within the given limits.

The area (A) can be calculated as:

`\displaystyle A = \int\limits^b_a {[\text{Upper Curve} \ - \ \text{Lower Curve}]} \, dx`

Where:

• Limits:
  `0\leq x\leq 3`
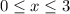
• Upper curve: y = 8x
• Lower curve: y = x

Plugging these into our integral we get:

`\Longrightarrow \displaystyle A = \int\limits^3_0 {(8x-x)} \, dx\\\\\\\\\Longrightarrow \boxed{\displaystyle A = \int\limits^3_0 {(7x)} \, dx}`

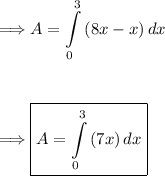
Now solving the integral, using the power rule of integration:

`\Longrightarrow \displaystyle A = \int\limits^3_0 {(7x)} \, dx\\\\\\\\\Longrightarrow \displaystyle A = 7\int\limits^3_0 {x} \, dx\\\\\\\\\Longrightarrow A = 7\Big[(1)/(2)x^2 \Big]^3_0\\\\\\\\\LongrightarrowA = 7\Big[(1)/(2)(3)^2- (1)/(2)(0)^2\Big]\\\\\\\\\Longrightarrow A= 7\Big[(9)/(2)\Big]\\\\\\\\\therefore \boxed{\boxed{A = (63)/(2) \ \text{or} \ 31.5 \ \text{units}^2 }}`

So, the area of the region enclosed by the graphs of the equations y = x, y = 8x, and x = 3 is 31.5 square units.

`\hrulefill`

Additional Information:

Integration: Integration is a mathematical operation that essentially involves finding the area under a curve or the accumulation of quantities. In this case, we are integrating to find the area of the enclosed region.

Limits of Integration: These are the values that determine the range over which the integration is performed. In this problem, the limits of integration are from 0 to 3, which means we are finding the area between x = 0 and x = 3.

Upper and Lower Curves: These terms refer to the curves that bound the region you're calculating the area for. The upper curve is y = x, and the lower curve is y = 8x in this problem.

Point of Intersection: This is where two curves cross each other.

Power Rule of Integration: The power rule of integration is a fundamental rule used in calculus to find the antiderivative (indefinite integral) of a function that is a power of a variable. It's closely related to the power rule for differentiation and is an essential tool for evaluating integrals of polynomial functions. The power rule states that:


`\boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\\displaystyle \int x^ndx=(x^(n+1))/(n+1) \end{array}\right}`