Answer: A. 61.12 in²
Explanation:
To solve the problem, let's start by finding the area of the right triangle. Finding the area of a right triangle is a lot like finding the area of a rectangle.
To find it, you need to multiply the length and height. So 8·9 is 72. To find the area of the triangle, divide that by 2, because a two right triangles make up a rectangle.
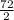=36 and 36 is the right triangle's area.
To find the area of the semicircle, we need to first find the radius. The radius the distance from the middle of the circle is any point on the edge. We know the diameter, which is the length from one end to the circle to the other. The diameter is 8.
Now the diameter is twice the radius, so our radius is 4. Now the formula to find the area of a circle is A=πr², but since we are substituting 3.14 for π, the formula is A=3.14r².
Since in GEMDAS, or order of operations, exponents come before multiplication, we have to do r² first. 4²=16 and 3.14·16=50.24. Now since this is a semicircle, and not a circle, we need to divide our area, 50.24 by 2, and we'll get 25.12 as our answer.
Now, we can finally add the right triangle area to the area of the semicircle, and 36+25.12=61.12, therefore confirming the answer.
Hope that helped a lot.
:)