Question

Write parametric equations that represent the following: a. The line segment from (−5,7) to (3,12) where the parameter (t) is on the interval 0≤t≤1. b. The circle centered on the origin with radius 5 traced exactly once counterclockwise. c. The circle centered on the origin with radius 5 traced exactly once clockwise where the parameter (t) is on the interval 0≤t≤1.

Answer 1

a. The parametric equations for the line segment from (-5, 7) to (3, 12) where the parameter t is on the interval
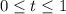`\(0 \leq t \leq 1\)` can be written as:

x(t) = -5 + 8t

y(t) = 7 + 5t

b. The parametric equations for the circle centered at the origin with radius 5 traced exactly once counterclockwise can be expressed using the trigonometric functions sine and cosine:

x(t) = 5 cos(t)

y(t) = 5 sin(t)

c. For the circle centered at the origin with radius 5 traced exactly once clockwise on the interval
`\(0 \leq t \leq 1\),` you can use the following parametric equations:

x(t) = 5 cos(
`2\pi` - t)

y(t) = 5 sin(2
`\pi` - t)