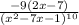Answer:
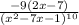
Explanation:
1. To derive a function we use the power rule, it states:
The derivative of
 is
is
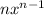
2. Furthermore since this function has x in brackets to a power we need to use the chain rule
 =
=
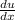 x
x
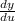
3. For this equation let
u =

y =

lets differentiate u first using the power rule
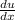 = 2x -7
= 2x -7
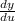 =
=
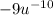
a negative exponent is simply
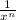 therefore
therefore
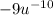 =
=
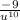
now we do
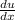 x
x
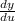
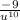 x 2x -7 =
x 2x -7 =
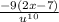
3. Now we replace the u with its original value