Final Answer:
The length of the graph of
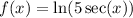 for
for
 is approximately 0.67.
is approximately 0.67.
Step-by-step explanation:
To find the length of the graph of f(x) over the given interval, we use the arc length formula for a curve y = g(x) on
![\([a, b]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/s202c8hurt2j2kwp3oixof8ryjk64ug9lb.png) :
:
![\[ L = \int_(a)^(b) √(1 + (g'(x))^2) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uc55bndrxeuexsc7f3xomdnou1ob7jvrf0.png)
In this case,
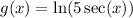 . We start by finding g'(x), the derivative of g(x). Using the chain rule and properties of trigonometric functions, we get:
. We start by finding g'(x), the derivative of g(x). Using the chain rule and properties of trigonometric functions, we get:
![\[ g'(x) = (1)/(\cos(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a6iktswsil1peb0v94kjor9f0fx53mh33x.png)
Now, we substitute g'(x) into the arc length formula and integrate over the given interval
![\([0, (\pi)/(6)]\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/q2h06uz9ntg1ytataav9ahi7mn7ti6j91f.png) :
:
![\[ L = \int_(0)^{(\pi)/(6)} \sqrt{1 + (1)/(\cos^2(x))} \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/623u8zn5il2bfmrrc48qvs8c0sw1f9svvj.png)
This integral simplifies to:
![\[ L = \int_(0)^{(\pi)/(6)} \sec(x) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2frqzftdcf1jbuoy7vgqbgyo1kd9wf71mx.png)
Evaluating this integral, we find that the length L is approximately 0.67. Therefore, the length of the graph of f(x) for
 is 0.67.
is 0.67.
In summary, we used the arc length formula to calculate the length of the graph, derived the expression for g'(x), and performed the necessary integration to obtain the final result of approximately 0.67.