Answer:
slope-intercept form:
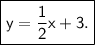
Slope (m):

Y-intercept (b): 3
Explanation:
The equation you provided is in standard form: 3x - 6y = -18.
In order to convert it into
 ,
,
where "m" is the slope and "b" is the y-intercept,
Follow this steps.
Start with the given equation:

Subtract 3x from both sides of the equation:
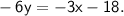
Divide both sides by -6:
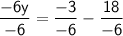
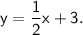
Now the equation is in slope-intercept form:
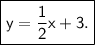
The slope (m) is the coefficient of the x-term, which is

This means that for every increase of 1 in the x-coordinate, the y-coordinate will increase by

The slope indicates the rate of change of the y-coordinate with respect to the x-coordinate.
The y-intercept (b) is the constant term in the equation, which is 3.
It represents the point where the graph of the line crosses the y-axis.
In other words, when x = 0, y = 3.
To summarize:
slope-intercept form:
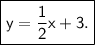
Slope (m):

Y-intercept (b): 3