The area of the region enclosed by the given curves is
![\(162\sqrt[3]{9}\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/7s4681yfwy65y0wgvoruxbo0ovgtq02pry.png) .
.
To find the area enclosed by the given curves, we need to determine the points where these curves intersect and set up the integral accordingly. Let's find the points of intersection by setting y equal for the two curves:
![\[9 \cos x = (9 \sec x)^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bqqewz127zzsw6xaukds73p6xn4nhz6wvm.png)
First, rewrite
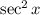 in terms of
in terms of
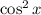 :
:
![\[9 \cos x = (1)/(\cos^2 x)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2zc9j9gab5ozf3nty2oozxpo98n0i33sgs.png)
Now multiply both sides by
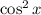 to get rid of the denominator:
to get rid of the denominator:
![\[9 \cos^3 x = 1\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wzumdu2caf6jxr7wd144gt75hrjciyjaw4.png)
Solve for
 :
:
![\[\cos x = \frac{1}{\sqrt[3]{9}}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/b1bc2qi2d34rk0ba59aucelvr9bb4g93an.png)
Now, the points of intersection are where
![\(x = \pm \arccos\left(\frac{1}{\sqrt[3]{9}}\right)\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/ewhyahkc61r07maxrpbc2tk57h3cf0iard.png) .
.
Now, we need to decide whether to integrate with respect to
 . Since the curves are defined in terms of
. Since the curves are defined in terms of
 as functions of
as functions of
 , it's more convenient to integrate with respect to
, it's more convenient to integrate with respect to
 .
.
The area
 is given by the integral:
is given by the integral:
![\[A = \int_(-\pi/4)^(\pi/4) \left((9\sec x)^2 - 9\cos x\right) \,dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jdicdscvbx5enw6g7sj3n3lb7b7khovat9.png)
Now, calculate this integral to find the area of the region.
Let's continue solving the integral to find the area of the region enclosed by the given curves.
![\[ A = \int_(-\pi/4)^(\pi/4) \left((9\sec x)^2 - 9\cos x\right) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qj0a8d7gp63v13fnlhfzt5l5yv47v2pib8.png)
We already found the points of intersection to be
![\(x = \pm \arccos\left(\frac{1}{\sqrt[3]{9}}\right)\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/ewhyahkc61r07maxrpbc2tk57h3cf0iard.png) . We'll use these as the limits of integration.
. We'll use these as the limits of integration.
![\[ A = \int_{-\arccos\left(\frac{1}{\sqrt[3]{9}}\right)}^{\arccos\left(\frac{1}{\sqrt[3]{9}}\right)} \left((9\sec x)^2 - 9\cos x\right) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hvrxsphekuwpyg8hmp03e2awu6h5kf81e5.png)
Now, simplify the expression inside the integral:
![\[ A = \int_{-\arccos\left(\frac{1}{\sqrt[3]{9}}\right)}^{\arccos\left(\frac{1}{\sqrt[3]{9}}\right)} \left((81)/(\cos^2 x) - 9\cos x\right) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/apcmvk41pp3qrh5ynpc3d6l9ueqa10rrwc.png)
To proceed, let's make a substitution to simplify the integral. Let
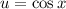 , then
, then
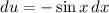 . Also, when
. Also, when
![\(x = -\arccos\left(\frac{1}{\sqrt[3]{9}}\right)\), \(u = -\frac{1}{\sqrt[3]{9}}\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/auyx4osguhdagi077qc9qodhj50xcv06wz.png) , and when
, and when
![\(x = \arccos\left(\frac{1}{\sqrt[3]{9}}\right)\), \(u = \frac{1}{\sqrt[3]{9}}\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/69qtfdtzdj0da2ra8xrqxhg9c81p35yl8c.png) .
.
![\[ A = \int_{-1/\sqrt[3]{9}}^{1/\sqrt[3]{9}} \left((81)/(u^2) - 9u\right) \, \left(-(1)/(\sin x)\right) \,du \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1rn8l0rd2nekovo5fmwi1ip7gzzobchtqj.png)
![\[ A = \int_{-1/\sqrt[3]{9}}^{1/\sqrt[3]{9}} \left((-81)/(u^2) + 9u\right) \, \csc x \,du \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/79bjj1hb2kp4mfs3xp3thtf61ba9suq5z3.png)
Now, integrate with respect to u:
![\[ A = \left[(81)/(u) + (9u^2)/(2)\right]_{-1/\sqrt[3]{9}}^{1/\sqrt[3]{9}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3sgp2raq8s875ulqhql9h6sfnj8b7jwszr.png)
Evaluate the expression at the upper and lower limits:
![\[ A = \left[\frac{81}{1/\sqrt[3]{9}} + \frac{9(1/\sqrt[3]{9})^2}{2}\right] - \left[\frac{81}{-1/\sqrt[3]{9}} - \frac{9(-1/\sqrt[3]{9})^2}{2}\right] \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4ysyrmw4y0xoni3ouqtgg0mq6oesys3z1b.png)
Simplify the expression:
![\[ A = 81\sqrt[3]{9} + (9)/(2)\sqrt[3]{9} - \left(-81\sqrt[3]{9} + (9)/(2)\sqrt[3]{9}\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/d6clcur9cnx1npc5ol6zci2zdm1bg1bstg.png)
Combine like terms:
![\[ A = 162\sqrt[3]{9} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tetywcyrkvu2i5x9lrep3zahpznrlartus.png)