Radian measure of the central angle AOB of the circle is 0.524 radians.
To find the radian measure of the central angle AOB in a circle, given the radius of the circle and the length of the arc AB , we'll follow these steps:
Step 1: Convert All Measurements to the Same Unit
The radius is given in inches, and the arc length is given in feet. We need to convert them to the same unit. Since there are 12 inches in a foot, we'll convert the arc length to inches.
Step 2: Use the Relationship Between Arc Length, Radius, and Central Angle
The formula relating the arc length L , the radius r , and the central angle
 in radians is:
in radians is:
![\[ L = r \theta \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/896lq4z4mw2pkmodzs36m1c3k3ixp9yeeu.png)
Step 3: Solve for the Central Angle
We rearrange the formula to solve for
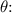
![\[ \theta = (L)/(r) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/c9irn66hmh6war8yrmk52k0s2yhzftbgaw.png)
Step 4: Calculate the Central Angle
We substitute the values of L (arc length) and r (radius) into the formula to find
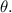
Let's start by converting the arc length to inches and then calculate the central angle.
The radian measure of the central angle AOB of the circle is approximately 0.524 radians.