Question

What is the sector area of an eighth of a circle on a circle with a radius of 10 feet? (Give your answer rounded to the nearest tenth. )

Answer 1

To find the sector area of an eighth of a circle, divide the area of the whole circle by 8. The approximate value of the sector area of an eighth of a circle on a circle with a radius of 10 feet is 39.3 square feet.

Step-by-step explanation:

To find the sector area of an eighth of a circle, you need to first find the area of the whole circle and then divide it by 8. The formula for the area of a sector is A = (θ/360) x πr², where θ is the central angle in degrees and r is the radius. In this case, the central angle for an eighth of a circle is 45 degrees. So, using a radius of 10 feet:

A = (45/360) x π(10)² = (1/8) x π(10)² = (1/8) x 100π ≈ 39.3 square feet

Answer 2

The sector area of an eighth of a circle with a radius of 10 feet is approximately 19.6 square feet, rounded to the nearest tenth.

Step-by-step explanation:

To find the sector area of an eighth of a circle, we can use the formula for the area of a sector:

`\[ \text{Sector Area} = (\theta)/(360^\circ) * \pi r^2 \]`

where
`\(\theta\)` is the central angle in degrees and \(r) is the radius. In this case, since we are dealing with an eighth of a circle, the central angle
`\(\theta\) is \(45^\circ\) (since \(360^\circ / 8 = 45^\circ\)).`

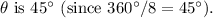
Now, substitute the values into the formula:

`\[ \text{Sector Area} = (45^\circ)/(360^\circ) * \pi * (10 \, \text{ft})^2 \]`

Simplifying the expression:

`\[ \text{Sector Area} = (1)/(8) * \pi * 100 \]`

Calculate the numerical value:

`\[ \text{Sector Area} \approx 19.6 \, \text{ft}^2 \]`

So, the sector area of an eighth of a circle with a radius of 10 feet is approximately 19.6 square feet, rounded to the nearest tenth.

This result signifies the portion of the circle enclosed by an eighth of its circumference. It's crucial to understand that the central angle, in this case, determines the fraction of the circle being considered. In mathematical terms, the fraction is
`\((1)/(8)\)` of the full circle, and the corresponding area is found by applying this fraction to the total area formula for a circle sector.