For
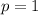 :
:
Original CPU time:
![\[ \text{CPU Time}_{\text{original}} = ((2.56 * 10^9 * 1 + 1.28 * 10^9 * 12 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/48dscsqkfvcjrah8y45p79jundnta9bme9.png)
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + 1.28 * 10^9 * 12 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/4iujqw3j474efjygghn5u6g43wnn4l4kfk.png)
2. For
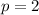 :
:
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + (1.28 * 10^9 * 12)/1.4 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/e8crq75p20c7oqya17i5jmhc4ns1ynr60x.png)
3. For
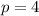 :
:
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + (1.28 * 10^9 * 12)/(2.8) + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/kyn31aksjaal3gs7adw3fg8e5kw0w9r2a2.png)
4. For
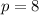 :
:
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + (1.28 * 10^9 * 12)/(5.6) + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/bgjslt3tu0t3bueetvis724b9pn8k9fntu.png)
To analyze the impact of doubling the CPI (Cycle Per Instruction) of arithmetic instructions on the execution time of a program, we need to use Amdahl's Law and the formula for CPU time:
![\[ \text{CPU Time} = \frac{\text{Instructions} * \text{CPI} * \text{Clock Cycles}}{\text{Clock Frequency}} \]](https://img.qammunity.org/2024/formulas/engineering/college/lsgmgdv7ml32pj1gky2hh9ekx3nlc18sex.png)
The parallelized portion is the arithmetic instructions, and the speedup is given by:
![\[ \text{Speedup} = (1)/(f + (1 - f)/(p)) \]](https://img.qammunity.org/2024/formulas/engineering/college/l9uyi8ftrzp6cz9ht20w9y0qhr5fs4rrqn.png)
where
 is the fraction of the program that is parallelized (in this case, the fraction of arithmetic instructions).
is the fraction of the program that is parallelized (in this case, the fraction of arithmetic instructions).
Let's calculate the original and new CPU times for each case when
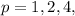 and
and
 , and analyze the impact on execution time:
, and analyze the impact on execution time:
Given:
- Number of arithmetic instructions =
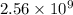
- Number of load/store instructions =
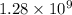
- Number of branch instructions =

- Clock frequency =
 GHz
GHz
- CPI for arithmetic instructions (original) =

- CPI for load/store instructions =

- CPI for branch instructions =

Original CPU time
 :
:
![\[ \text{CPU Time}_{\text{original}} = ((2.56 * 10^9 * 1 + 1.28 * 10^9 * 12 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/48dscsqkfvcjrah8y45p79jundnta9bme9.png)
Now, let's calculate the new CPU times for
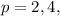 and
and
 with the doubled CPI for arithmetic instructions
with the doubled CPI for arithmetic instructions
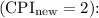
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + 1.28 * 10^9 * 12 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/4iujqw3j474efjygghn5u6g43wnn4l4kfk.png)
For
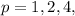 and
and
 , compare the new CPU times with the original CPU time to determine the impact:
, compare the new CPU times with the original CPU time to determine the impact:
![\[ \text{Speedup} = \frac{\text{CPU Time}_{\text{original}}}{\text{CPU Time}_{\text{new}}} \]](https://img.qammunity.org/2024/formulas/engineering/college/7a15d22u8kdk0h18zcybmfwvru1uyp27rj.png)
Now, let's calculate:1. For
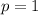 :
:
Original CPU time:
![\[ \text{CPU Time}_{\text{original}} = ((2.56 * 10^9 * 1 + 1.28 * 10^9 * 12 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/48dscsqkfvcjrah8y45p79jundnta9bme9.png)
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + 1.28 * 10^9 * 12 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/4iujqw3j474efjygghn5u6g43wnn4l4kfk.png)
2. For
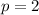 :
:
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + (1.28 * 10^9 * 12)/1.4 + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/e8crq75p20c7oqya17i5jmhc4ns1ynr60x.png)
3. For
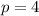 :
:
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + (1.28 * 10^9 * 12)/(2.8) + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/kyn31aksjaal3gs7adw3fg8e5kw0w9r2a2.png)
4. For
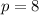 :
:
New CPU time:
![\[ \text{CPU Time}_{\text{new}} = ((2.56 * 10^9 * 2 + (1.28 * 10^9 * 12)/(5.6) + 256 * 10^6 * 5))/(2 * 10^9) \]](https://img.qammunity.org/2024/formulas/engineering/college/bgjslt3tu0t3bueetvis724b9pn8k9fntu.png)
Calculate the speedup for each case:
![\[ \text{Speedup} = \frac{\text{CPU Time}_{\text{original}}}{\text{CPU Time}_{\text{new}}} \]](https://img.qammunity.org/2024/formulas/engineering/college/7a15d22u8kdk0h18zcybmfwvru1uyp27rj.png)
Now, let's calculate each speedup using the original and new CPU times:
![\[ \text{Speedup} = \frac{\text{CPU Time}_{\text{original}}}{\text{CPU Time}_{\text{new}}} \]](https://img.qammunity.org/2024/formulas/engineering/college/7a15d22u8kdk0h18zcybmfwvru1uyp27rj.png)
1. For
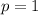 :
:
![\[ \text{Speedup}_(p=1) = \frac{\text{CPU Time}_{\text{original}}}{\text{CPU Time}_{\text{new}}, p=1} \]](https://img.qammunity.org/2024/formulas/engineering/college/u9ilrono9gfcaboog59zomz3n28vr6eohm.png)
2. For
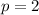 :
:
![\[ \text{Speedup}_(p=2) = \frac{\text{CPU Time}_{\text{original}}}{\text{CPU Time}_{\text{new}}, p=2} \]](https://img.qammunity.org/2024/formulas/engineering/college/5oml5ozzvxmlpw4hhv2o72q7gob3xiuvz3.png)
3. For
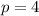 :
:
![\[ \text{Speedup}_(p=4) = \frac{\text{CPU Time}_{\text{original}}}{\text{CPU Time}_{\text{new}}, p=4} \]](https://img.qammunity.org/2024/formulas/engineering/college/l6cteh0ecfv519ljw726bxflqqsqbnetdv.png)
4. For
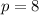 :
:
![\[ \text{Speedup}_(p=8) = \frac{\text{CPU Time}_{\text{original}}}{\text{CPU Time}_{\text{new}}, p=8} \]](https://img.qammunity.org/2024/formulas/engineering/college/w42eynhi7erate5672i40bmb2h7ye5n1fc.png)