Question

Find the volume V of the described solid S. The base of S is a circular disk with radius 5r. Parallel cross-sections perpendicular to the base are squares.

Answer 1

To find the volume V of the solid S, calculate the volume of the cylinder formed by the circular disk. The radius of the base is given as 5r and the cross-sectional area of the squares is 4r².

Step-by-step explanation:

The volume of the solid S can be found by calculating the volume of the cylinder formed by the circular disk, which serves as the base. The formula for the volume of a cylinder is V = πr²h, where r is the radius of the base and h is the height of the cylinder. In this case, the radius is given as 5r, so we substitute 5r for r in the formula. The cross-sectional area A of the squares perpendicular to the base is equal to the area of a square with side length 2r, which is (2r)² = 4r². Therefore, the volume V of the solid S is V = Ah = 4r²h.

Answer 2

The volume V of the solid S is
`625r^4 / 3`.

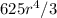To find the volume V of the solid S, we can use the method of slicing:

Imagine slicing S horizontally into thin squares. Each square will have a side length dependent on its distance from the center of the base. Let x be the distance from the center of the base, and s(x) be the side length of the square at that distance.

Find the area of each square. Since each square is parallel to the base, its side length s(x) is related to the base radius (5r) by the Pythagorean theorem. Here's the equation:

`[s(x)]^2 + x^2 = (5r)^2`

Solving for s(x), we get:

`s(x) = √((25r^2 - x^2))`

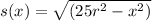
Calculate the area of each square:

`A(x) = [s(x)]^2 = 25r^2 - x^2`

Treat each square as a thin prism with thickness dx. The volume of each prism is:

`dV(x) = A(x) dx = (25r^2 - x^2) dx`

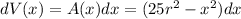
Integrate the volume of each prism from the edge of the base (x = -5r) to the center (x = 0):

`V = \int_(-5r)^(0) (25r^2 - x^2) dx`

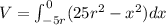
Solve the integral:

`V = \int_(-5r)^(0) (25r^2 - x^2) dx = [25rx^3 - x^3/3]_(-5r)^(0) = 625r^4/3`