 is true based on the given statements and the information derived from them.
is true based on the given statements and the information derived from them.
We are given that
 . From this, we can infer that F is true and O is also true.
. From this, we can infer that F is true and O is also true.
Now, let's use the first statement:
 . This statement says that if F is true, then both
. This statement says that if F is true, then both
 and A are true.
and A are true.
Since we know that F is true, we can conclude that
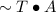 is true. This means that both
is true. This means that both
 and A are true.
and A are true.
Moving on to the second statement:
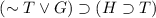 . This statement says that if either
. This statement says that if either
 or G is true, then
or G is true, then
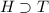 is true.
is true.
Now, let's consider the third statement:
 . This statement says that both
. This statement says that both
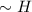 and
and
 are true.
are true.
Based on the second statement, we know that if either
 or G is true, then
or G is true, then
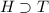 is true. Since we have
is true. Since we have
 as true from the third statement, we can conclude that
as true from the third statement, we can conclude that
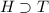 is true.
is true.
Finally, combining the information from the first and second statements, we have
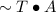 and
and
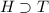 as true. This means that both
as true. This means that both
 and A are true, and
and A are true, and
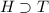 is true.
is true.