Question

The graphs of which functions are increasing from the right to the left and decreasing from the left to the right? Select all that apply. Select all that apply: o f(x) = -4x3 O f(x) = -8x+ + 7 Of(x) = 9x3 + 7x2 + 11 f(x) = 14x6 + 8x3 + 7x + 11 Of(x) = -x5 + 8x4 + 9x3 + 36 O f(x) = 7x6 + 8x5 + 11x4 – 6x5 + 125

Answer 1

The function that matches the criteria (increasing as we move from right to left and decreasing as we move from left to right) is
`\( f(x) = -8x^2 + 7 \).`

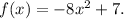
To determine which functions are increasing as we move from right to left and decreasing as we move from left to right, we need to analyze the end behavior of the functions based on their leading terms. For polynomial functions, the end behavior is primarily determined by the term with the highest degree (the leading term).

1.
`\( f(x) = -4x^3 \)`: This is a cubic function with a negative leading coefficient. Cubic functions with a negative leading coefficient decrease as x goes to positive infinity and increase as x goes to negative infinity. Does not applies.

2.
`\( f(x) = -8x^2 + 7 \)`: This is a quadratic function with a negative leading coefficient. Quadratic functions with a negative leading coefficient open downwards, meaning they increase as x goes to negative infinity and decrease as x goes to positive infinity. Applies.

3.
`\( f(x) = 9x^3 + 7x^2 + 11 \)`: This is a cubic function with a positive leading coefficient. Cubic functions with a positive leading coefficient increase as x goes to positive infinity and decrease as x goes to negative infinity. Does not apply.

4.
`\( f(x) = 14x^6 + 8x^3 + 7x + 11 \)`: This is a polynomial function of degree 6 with a positive leading coefficient. Even-degree polynomial functions with positive leading coefficients increase as x goes to both positive and negative infinity. Does not apply.

5
`. \( f(x) = -x^5 + 8x^4 + 9x^3 + 36 \)`: This is a polynomial function of degree 5 with a negative leading coefficient. Odd-degree polynomial functions with negative leading coefficients decrease as x goes to positive infinity and increase as x goes to negative infinity. Does not apply.

6.
`\( f(x) = 7x^6 + 8x^5 + 11x^4 - 6x^3 + 125 \)` : This is a polynomial function of degree 6 with a positive leading coefficient. Even-degree polynomial functions with positive leading coefficients increase as x goes to both positive and negative infinity. Does not apply.