Final Answer:
The exponential model representing the given points
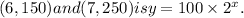
Step-by-step explanation:
To construct an exponential model, we can use the general form
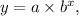 where
where
 is the initial value or y-intercept,
is the initial value or y-intercept,
 is the base of the exponential function, and
is the base of the exponential function, and
 is the independent variable. Given the points (6, 150) and (7, 250), we can use the values to determine the specific coefficients of the model.
is the independent variable. Given the points (6, 150) and (7, 250), we can use the values to determine the specific coefficients of the model.
Starting with the point (6, 150), we substitute
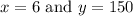 into the general form:
into the general form:
![\[150 = a * b^6\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hsqrg82qzpbaow3kds7m1eahcxa0dphm3h.png)
Similarly, for the point (7, 250):
![\[250 = a * b^7\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wja7veb6wi7hk5zsk1qnp87u846m79wtwu.png)
Dividing the second equation by the first eliminates
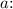
![\[(250)/(150) = (a * b^7)/(a * b^6)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8sz3b7g3tx8vyhjsc51p4uj66364jb340t.png)
Simplifying, we get:
![\[(5)/(3) = b\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/i9djh4idkierayk74tj122ajrjeiqnvqyk.png)
Now, substitute
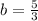 into the first equation to find
into the first equation to find
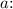
![\[150 = a * \left((5)/(3)\right)^6\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v6voausjfokr3e79o3zmf1a7agasyp9lno.png)
Solving for
 , we get:
, we get:
![\[a = 100\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x1lxt1owvrcd0ahmg5pe6g9zbvzpgwwhht.png)
Therefore, the exponential model is
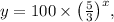 which can be simplified to
which can be simplified to
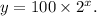 This model accurately represents the exponential growth exhibited by the given data points.
This model accurately represents the exponential growth exhibited by the given data points.