The reference number for t = 5 is 0.
To find the reference number for each value of t, you'll need to calculate the corresponding trigonometric ratios for the given angles. The reference number is essentially the value of the trigonometric function in the standard position (angle measured from the positive x-axis to the terminal side of the angle) for the given angle t. Here's how you can do it for each value of t:
(a)
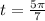
To find the reference number for
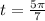 , follow these steps:
, follow these steps:
1. Determine the reference angle
 by finding the acute angle formed between the terminal side of t and the positive x-axis. In this case, t is already an acute angle, so
by finding the acute angle formed between the terminal side of t and the positive x-axis. In this case, t is already an acute angle, so
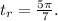
2. Since t is in the second quadrant
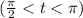 , the reference number for t will be the same as for its reference angle
, the reference number for t will be the same as for its reference angle

So, the reference number for
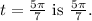
(b)
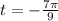
To find the reference number for
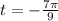 , follow these steps:
, follow these steps:
1. Determine the reference angle
 by finding the acute angle formed between the terminal side of t and the positive x-axis. In this case, t is in the third quadrant, so the reference angle is
by finding the acute angle formed between the terminal side of t and the positive x-axis. In this case, t is in the third quadrant, so the reference angle is
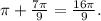
2. Since t is in the third quadrant
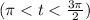 , the reference number for t will be the negative of its reference angle
, the reference number for t will be the negative of its reference angle

So, the reference number for
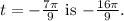
(c) t = -3
To find the reference number for t = -3, follow these steps:
1. Determine the reference angle
 by finding the acute angle formed between the terminal side of t and the positive x-axis. Since t is negative and lies along the negative x-axis, there is no reference angle in this case.
by finding the acute angle formed between the terminal side of t and the positive x-axis. Since t is negative and lies along the negative x-axis, there is no reference angle in this case.
2. In this case, since there's no reference angle, the reference number for t is 0 because it lies along the negative x-axis.
So, the reference number for
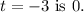
(d)

To find the reference number for
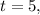 follow these steps:
follow these steps:
1. Determine the reference angle
 by finding the acute angle formed between the terminal side of t and the positive x-axis. Since t is positive and lies along the positive x-axis, there is no reference angle in this case.
by finding the acute angle formed between the terminal side of t and the positive x-axis. Since t is positive and lies along the positive x-axis, there is no reference angle in this case.
2. In this case, since there's no reference angle, the reference number for t is also 0 because it lies along the positive x-axis.