Question

A model rocket is launched with an initial upward velocity of 57 m/s. The rocket's height h (in meters) after t seconds is given by the following. h=571-58 Find all values of t for which the rocket's height is 29 meters. Round your answer(s) to the nearest hundredth. (If there is more than one answer, use the "or" button.) 0 seconds or Х h ground

Answer 1

The rocket's height is 29 meters at approximately t = 0.24 seconds and t = 9.86 seconds.

Step-by-step explanation:

To find the values of t when the rocket's height is 29 meters, we set the height function
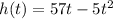`\( h(t) = 57t - 5t^2 \)`equal to 29 and solve for t . The equation becomes:

`\[ 57t - 5t^2 = 29. \]`

Rearranging and setting the equation to zero, we get:

`\[ 5t^2 - 57t + 29 = 0. \]`

Now, we can use the quadratic formula to find the values of t :

`\[ t = (-b \pm √(b^2 - 4ac))/(2a). \]`

In this case, a = 5, b = -57, and c = 29 . Plugging in these values and solving, we find
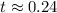`\( t \approx 0.24 \)` seconds or
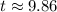`\( t \approx 9.86 \)`seconds.

The two solutions represent the times at which the rocket's height is 29 meters. The positive root
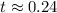`\( t \approx 0.24 \)` seconds corresponds to the initial ascent of the rocket, while the second root
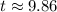`\( t \approx 9.86 \)` seconds represents the time when the rocket reaches a height of 29 meters again during its descent. Therefore, these are the values of t for which the rocket's height is 29 meters.