It will take approximately 1.69 minutes (rounded to two decimal places) for the thermometer to reach 35°F when taken outside.
To solve this problem, we can use Newton's Law of Cooling, which describes how the temperature of an object changes when it is removed from one environment (in this case, a room) and exposed to a different environment (outside). The law is given by the formula:
![\[T(t) = T_e + (T_0 - T_e) \cdot e^(-kt)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/quhrtnd2nwu3vbhfmh4hpsedyclr3jeubq.png)
Where:
 is the temperature of the object at time t.
is the temperature of the object at time t.
 is the temperature of the environment (outside).
is the temperature of the environment (outside).
 is the initial temperature of the object when it was removed from the room.
is the initial temperature of the object when it was removed from the room.
k is a constant that depends on the object and the environment.
Given:
 (initial temperature) = 70°F
(initial temperature) = 70°F
 (outside temperature) = 30°F
(outside temperature) = 30°F
- After 30 seconds (t = 0.5 minutes), the thermometer reads 50°F.
We need to find the value of k first using the information at t = 0.5 minutes:
![\[50 = 30 + (70 - 30) \cdot e^(-0.5k)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9ji20i7wr4u5k9ikuhidrprw3oy579e0g3.png)
Let's solve for k:
![\[20 = 40 \cdot e^(-0.5k)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hqdqhf53zxqe3glx0c41uowkguxs2ppd8d.png)
Now, divide both sides by 40:
![\[0.5 = e^(-0.5k)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jtsow4c92wl8b1z03abu8vp4bgd70z0dz8.png)
Take the natural logarithm (ln) of both sides to isolate k:
![\[\ln(0.5) = \ln(e^(-0.5k))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7dviecxf6dso06q7lnyzrgewgguqlu5cup.png)
Using the property of logarithms
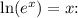
![\[\ln(0.5) = -0.5k\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5xujcq2q49huezo0jug54v10jx6tzy9nrq.png)
Now, solve for k:
![\[k = -(\ln(0.5))/(0.5)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9zzhhceoq23ye5iu2tp19ypxw576yzvz54.png)
Calculate k:
![\[k ≈ 1.3863\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jv2wmoyvsd79sxly6wrp89172l5ozqe42u.png)
Now that we have the value of k, we can use it to find when the thermometer reaches 35°F:
![\[35 = 30 + (70 - 30) \cdot e^(-kt)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nnyg03cestifnsfrjnn8zi5e9oh6qqwet7.png)
Substitute the known values:
![\[5 = 40 \cdot e^(-1.3863t)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wvxgjnxxqti23px8yreo34qmjhi890d8ah.png)
Divide both sides by 40:
![\[0.125 = e^(-1.3863t)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fta2acaq5y7pu1di49kk3y78sbq6mtagiz.png)
Take the natural logarithm (ln) of both sides:
![\[\ln(0.125) = \ln(e^(-1.3863t))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/myjnvx7chnk3gn6rf5ju8vealnfccj1tm5.png)
Using the property of logarithms
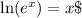 :
:
![\[\ln(0.125) = -1.3863t\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vxw1eg1ukcf6pn9w275lcazqbmvt857vux.png)
Now, solve for t:
![\[t = (\ln(0.125))/(-1.3863)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/egajlsdkr046ybnnb3l2lkte3scfbkto5j.png)
Calculate t:
![\[t ≈ 1.6931\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x1sefimtqutpctznzmf0mx0w8uuflm8mz0.png)