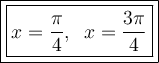Question

Identify the vertical asymptotes of each function. f(x)=tan(2x) on the interval [0, π]

Answer 1

`x=(\pi)/(4),\;\;x= (3\pi)/(4)`

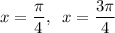
Explanation:

The tangent function can be expressed as the ratio of the sine function and cosine function:

`\tan x=(\sin x)/(\cos x)`

An asymptote is a line that the curve gets infinitely close to, but never touches.

When the denominator of a rational function is zero, the function is undefined. Therefore, y = tan x has vertical asymptotes when cos x = 0.

This means that the function f(x) = tan(2x) has vertical asymptotes when cos(2x) = 0 since:

`\tan (2x)=(\sin (2x))/(\cos (2x))`

Solve cos(2x) = 0:

`\begin{aligned}\cos(2x)&=0\\\\2x&=cos(-1)(0)\\\\x&=(\pi)/(2)+2\pi n, (3\pi)/(2)+2\pi n\\\\x&=(\pi)/(4)+\pi n, (3\pi)/(4)+\pi n\end{aligned}`

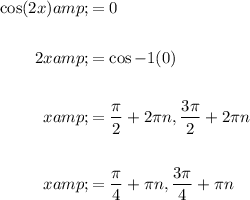
Therefore, the vertical asymptotes of f(x) = tan(2x) on the interval [0, π] are:

`\large\boxed{\boxed{x=(\pi)/(4),\;\;x= (3\pi)/(4)}}`