Question

Solve 9x*2 + 12x - 24 = 0 using the quadratic formula

Answer 1

`x=(2√(7) -2)/(3) \ \text{and} \ x=(-2 -2√(7))/(3)`

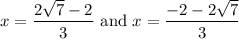
Explanation:

To solve the quadratic equation 9x² + 12x - 24 = 0 using the quadratic formula, follow these steps:

`\hrulefill`

The quadratic formula is given by:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Quadratic Formula:}}\\\\x=(-b\pm√(b^2-4ac) )/(2a) \end{array}\right}`

Where 'a,' 'b,' and 'c' are the coefficients of a quadratic equation in the form of ax² + bx + c = 0.

`\hrulefill`

In your equation, the coefficients are:

a = 9

b = 12

c = -24

(1) Plug these values into the quadratic formula:

`\Longrightarrow x=(-12\pm√((12)^2-4(9)(-24)) )/(2(9))`

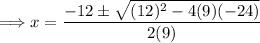
(2) Simplify the values within the square root:

`\Longrightarrow x=(-12\pm√(144+864) )/(18)\\\\\\\\\Longrightarrow x=(-12\pm√(1008) )/(18)`

(3) Calculate the square root of 1008:

`\Longrightarrow √(1008) = 12√(7)`

`\Longrightarrow x=(-12\pm12√(7) )/(18)`

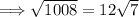
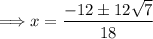
(4) Simplify both solutions:

`\Longrightarrow x_1=(-12+12√(7) )/(18)\\\\\\\\\Longrightarrow x_1=(-2+2√(7) )/(3)\\\\\\\\\therefore \boxed{x_1=(2√(7) -2)/(3) }`

`\Longrightarrow x_2=(-12-12√(7) )/(18)\\\\\\\\\Longrightarrow x_2=(-2-2√(7) )/(3)\\\\\\\\\therefore \boxed{x_2=(-2 -2√(7))/(3) }`

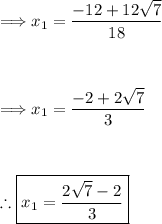
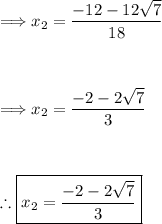
So, the solutions for the equation 9x² + 12x - 24 = 0 are:

`x=(2√(7) -2)/(3) \ \text{and} \ x=(-2 -2√(7))/(3)`

`\hrulefill`

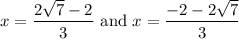
Additional Information:

Quadratic Equation: A quadratic equation is a polynomial equation of the second degree (having the highest power of the variable as 2). It can be written in the general form ax² + bx + c = 0, where a, b, and c are constants.

Quadratic Formula: The quadratic formula is a formula that gives the solutions (roots) of a quadratic equation directly. It is applicable for any quadratic equation in the standard form, ax² + bx + c = 0, where "a" is not equal to 0.

Discriminant: In the quadratic formula, the value inside the square root, b² - 4ac, is called the discriminant. It determines the nature of the roots of the quadratic equation. If the discriminant is positive, the equation has two distinct real roots. If it's zero, the equation has one real root (a repeated root). If it's negative, the equation has two complex conjugate roots (non-real).

Real Roots: Roots that are real numbers, meaning they can be found on the number line.

Complex Roots: Roots that involve the imaginary unit "i," where i² = -1. Complex roots come in pairs as complex conjugates.

Coefficient: The numerical factor that multiplies a variable term in a polynomial. In the equation ax² + bx + c = 0, "a," "b," and "c" are coefficients.