Question

Need help fast. here is screenshot

Answer 1

Parallel

Explanation:

In order to determine if the provided lines are parallel, perpendicular, or neither, it is necessary to analyze their slopes.

`\hrulefill`

Remember the slope-intercept form of a linear equation, which is given as:

`\boxed{\left\begin{array}{ccc}\text{\underline{Slope-Intercept Form:}}\\\\y=mx+b\end{array}\right }`

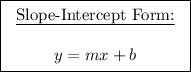
Where the value 'm' signifies the slope of the line.

• If two lines share the same slope, they are parallel to each other.
• If the slopes of two lines are negative reciprocals of one another, then these lines are perpendicular.
• If the slopes don't match either of these conditions, it means that the lines are neither parallel nor perpendicular to each other.

`\hrulefill`

Given lines:

y = 3x + 2

2y = 6x - 6

Equation (1) is already in slope-intercept form. Let's start by rearranging the second equation to the slope-intercept form:

(2)

Solve for 'y':

⇒ 2y = 6x - 6

∴ y = 3x - 3

Now, we can clearly see that both equations are in the slope-intercept form.

Equation 1 has a slope of 3.

Equation 2 also has a slope of 3.

Since both equations have the same slope (3), the lines the represent are parallel.

`\hrulefill`

Additional Information:

Reciprocal: The reciprocal of a numeric value is obtained by dividing 1 by that number. In mathematical terms, for any non-zero value 'a', its reciprocal 'b' can be expressed as:

• b = 1 / a

Negative Reciprocal: The negative reciprocal of a number is derived by taking the reciprocal of the number and then applying a negation, resulting in a negative value. Therefore, if 'a' represents a non-zero number, its negative reciprocal 'c' can be defined as:

• c = -1 / a